Абсолютная и относительная шероховатость труб
Абсолютная, эквивалентная и относительная шероховатость. Гидравлически гладкие и гидравлически шероховатые трубы.
На потери напора по длине при турбулентном режиме может оказывать влияние шероховатость стенок. ее обозначают k (или Δ). Абсолютной шероховатостью k называют среднюю высоту выступов шероховатости. Опыты показали, что при одной и той же величине абсолютной шероховатости влияние ее на величину гидравлического сопротивления различно в зависимости от диаметра трубы. Поэтому вводится величина относительной шероховатости . Относительной шероховатостью называется отношение абсолютной шероховатости к диаметру трубы, т.е. 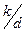 . Под эквивалентной шероховатостью Эта шероховатость пред ставляет собой выступы равномерно распределенной зернис той абсолютной шероховатости такого размера, который дает при подсчетах одинаковые с действительной шероховатостью потери напора. Значения эквивалентной шероховатости опре деляют на основании гидравлических испытаний трубопроводов и пересчета их результатов по соответствующим формулам. При практических расчетах значения эквивалентной шеро ховатости принимают с учетом материала трубы и ее состояния, зависящего, в частности, от продолжительности и условий эксплуатации . Под эквивалентной шероховатостью Эта шероховатость пред ставляет собой выступы равномерно распределенной зернис той абсолютной шероховатости такого размера, который дает при подсчетах одинаковые с действительной шероховатостью потери напора. Значения эквивалентной шероховатости опре деляют на основании гидравлических испытаний трубопроводов и пересчета их результатов по соответствующим формулам. При практических расчетах значения эквивалентной шеро ховатости принимают с учетом материала трубы и ее состояния, зависящего, в частности, от продолжительности и условий эксплуатации | |||||||||||
Трубы называют гидравлически гладкими, если шероховатость не влияет на их гидравлическое сопротивление. Для них используют эмпирические формулы: формулу П.К.Конакова для диапазона изменения критерия Рейнольдса от критического до нескольких миллионов 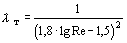 формулу Блазиуса для 2300 5 формулу Блазиуса для 2300 5 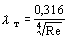 К гидравлически гладким трубам относят цельнотянутые трубы из цветных металлов, а также стальные высококачественные бесшовные трубы. На сопротивление шероховатых труб оказывает влияние критерий Рейнольдса, относительная шероховатость и ее характер. Равномерно распределенная зернистая шероховатость имеет один и тот же размер и форму бугорков при ламинарном течении шероховатость стенок канала на сопротивление влияния не оказывает; критическое значение критерия Рейнольдса от шероховатости практически не зависит; в области турбулентного течения при небольших значениях Re и малых D/d шероховатость на сопротивление не влияет. Однако с увеличениемRe это влияние начинает проявляться; при большихD/d и высоких значениях критерия Рейнольдса коэффициент сопротивления перестает зависеть отRe и становится постоянным для данного значения D/d. Для труб с реальной шероховатостью, в которых бугорки имеют различную высоту и, при увеличении значения критерия Рейнольдса, начинают выступать за пределы ламинарного подслоя не одновременно, переход от линии, соответствующей сопротивлению гладких труб, к прямым горизонтальным участкам происходит более плавно. Для практических расчетов коэффициента сопротивления шероховатых труб используют формулу А.Д.Альтшуля К гидравлически гладким трубам относят цельнотянутые трубы из цветных металлов, а также стальные высококачественные бесшовные трубы. На сопротивление шероховатых труб оказывает влияние критерий Рейнольдса, относительная шероховатость и ее характер. Равномерно распределенная зернистая шероховатость имеет один и тот же размер и форму бугорков при ламинарном течении шероховатость стенок канала на сопротивление влияния не оказывает; критическое значение критерия Рейнольдса от шероховатости практически не зависит; в области турбулентного течения при небольших значениях Re и малых D/d шероховатость на сопротивление не влияет. Однако с увеличениемRe это влияние начинает проявляться; при большихD/d и высоких значениях критерия Рейнольдса коэффициент сопротивления перестает зависеть отRe и становится постоянным для данного значения D/d. Для труб с реальной шероховатостью, в которых бугорки имеют различную высоту и, при увеличении значения критерия Рейнольдса, начинают выступать за пределы ламинарного подслоя не одновременно, переход от линии, соответствующей сопротивлению гладких труб, к прямым горизонтальным участкам происходит более плавно. Для практических расчетов коэффициента сопротивления шероховатых труб используют формулу А.Д.Альтшуля 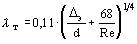 , где Dэ — эквивалентная абсолютная шероховатость (реальная шероховатость, которая оказывает такое же воздействие, что и равномерная зернистая шероховатость в опытах И.И.Никурадзе). Характерные значения Dэ для труб из различных материалов , где Dэ — эквивалентная абсолютная шероховатость (реальная шероховатость, которая оказывает такое же воздействие, что и равномерная зернистая шероховатость в опытах И.И.Никурадзе). Характерные значения Dэ для труб из различных материалов
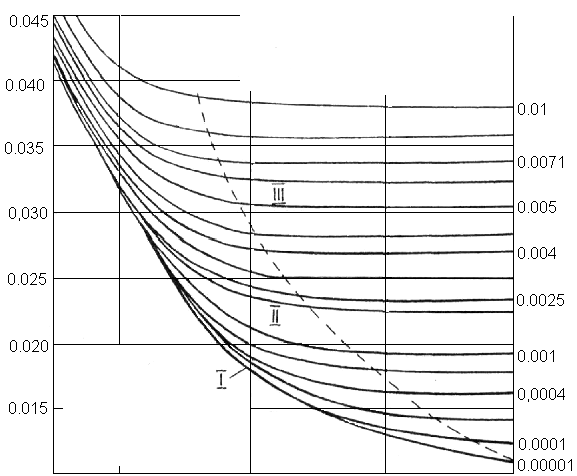
Для труб, отличающихся по форме от цилиндрических, вводят понятие гидравлического (эквивалентного) диаметра. Гидравлический диаметр — это диаметр круглой трубы, имеющей площадь поперечного сечения, равную площади трубы иной формы где П — полный смоченный периметр трубы. Гидравлический диаметр используют в формулах для расчета потерь давления в трубах, форма поперечного сечения которых отличается от круга. 10. Экспериментальные результаты по определению потерь при турбулентном движении жидкостиС точки зрения инженерных приложений главными являются следующие задачи: а) как определить потери напора (энергии); б) как распределены скорости по сечению трубы. 10.1. Абсолютная и относительная шероховатостьНа потери напора по длине при турбулентном режиме может оказывать влияние шероховатость стенок. Под шероховатостью будем понимать присутствие у любой поверхности неровностей (выступы и впадины). При заводском изготовлении труб шероховатость их внутренних стенок носит нерегулярный характер, как по высоте, так и по расположению, и поэтому одним параметром охарактеризована быть не может. Несмотря на это, в технических расчетах выбирают единственный параметр, а именно среднюю высоту выступов шероховатости; ее обозначают k (или Δ). Абсолютной шероховатостью k называют среднюю высоту выступов шероховатости. Опыты показали, что при одной и той же величине абсолютной шероховатости влияние ее на величину гидравлического сопротивления различно в зависимости от диаметра трубы. Поэтому вводится величина относительной шероховатости Относительной шероховатостью называется отношение абсолютной шероховатости к диаметру трубы, т.е. 10.2. Закономерности изменения коэффициента гидравлического тренияПотери напора по длине трубопровода обычно находят по формуле (9.14). При этом основной задачей является определение коэффициента гидравлического трения Re = На рис. 10.1 представлен экспериментальный график зависимости коэффициента На графике можно выделить три области: I — область гидравлически гладких труб, соответствующую сравнительно малым числам Рейнольдса, II — область доквадратичного сопротивления, III — область квадратичного сопротивления. В области гидравлически гладких труб коэффициент Red
Рис. 10.1. График Мурина – Шевелёва 10.3. Зависимости для коэффициента гидравлического сопротивления и области их примененияДля определения потерь по длине применяется формула Дарси-Вейсбаха h1 = λ Чтобы выбрать соответствующую зависимость для λ, предлагается простой алгоритм. Обычно заданы: расход Q, диаметр трубы d, кинематический коэффициент вязкости ν и величина эквивалентной шероховатости kэ (из таблиц) для данного материала. В табл. 10.1 приведены значения kэ для труб из разных материалов. Трубы, их материалы и состояние стенок k, мм Стальные цельнотянутые новые Стальные цельнотянутые, находившиеся в эксплуатации Стальные цельнотянутые после продолжительной эксплуатации, сильно заржавленные Чугунные асфальтированные новые Чугунные, находившиеся в эксплуатации а) среднюю скорость V= б) число Рейнольдса Rе = в) относительную шероховатость 1. Если Rе 4000, то определяют величину параметра Rе 3. Если Rе λ = 0,11 Задача 10.1. Определить, какой степени средней скорости пропорциональны потери по длине в каждой из зон сопротивления. Решение. Используется формула Дарси-Вейсбаха (9.14) и зависимость для 1. Для ламинарного режима
В правой части последней формулы первый сомножитель не зависит от скорости и величина hl имеет вид hl = 2. В зоне квадратичного сопротивления λ определяется по формуле λ=0,11 Так как первый сомножитель в правой части не зависит от скорости, то потери hl пропорциональны скорости в квадрате, откуда и название зоны – квадратичная зона сопротивления. Задача 10.2. Поток в трубе находится в квадратичной зоне сопротивления. Как изменятся потери по длине в этой трубе, если расход в ней увеличить в два раза? Решение. Учитывая решение задачи 10.1, заключаем, что если расход увеличить в два раза, то и средняя скорость увеличится в два раза и поэтому (поскольку зона квадратичная) потери возрастут в 2 2 , т.е. в 4 раза. Задача 10.3. Отрезок трубы внутренним диаметром d1=100 мм был заменен отрезком трубы такой же длины, но внутренним диаметром d2, в 2 раза меньшим: d2=50 мм. Определить, как изменились потери на этом участке при такой замене. Расход воды остался таким же; считаем для упрощения решения, что в обоих случаях квадратичный режим, изменение λ не учитываем. Решение. Для решения задачи достаточно определить отношение потерь h1 в трубе с d1=100 мм к h2 в трубе с d2=50 мм. Выражения для h1 и h2 по формуле Дарси-Вейсбаха (9.14)
Согласно уравнению неразрывности
Если возведем обе части последнего равенства в квадрат, получим
Подставляя (10.6) в (10.5), имеем окончательно Если
Таким образом, потери увеличились в 32 раза! Если учесть, что Этот же результат возможно получить, оценивая порядок величин, а именно, потери выражаются зависимостью
Средняя скорость выражается так V=Q/S или V 1/d 2 , т.е. при 1/d 4 . (10.8) Имея в виду (10.7) и (10.8), получаем в данном случае 1/d 5 , т.е. потери обратно пропорциональны диаметру в пятой степени. Этот результат имеет большое значение при гидравлических расчетах водопроводных сетей. Что такое относительная и абсолютная шероховатость?Содержание:
Относительная шероховатость и абсолютная шероховатость — это два термина, которые используются для описания набора существующих неровностей внутри промышленных труб, по которым транспортируются жидкости. Абсолютная шероховатость — это среднее или среднее значение этих неровностей, переведенное в среднее изменение внутреннего радиуса трубы. Абсолютная шероховатость считается свойством используемого материала и обычно измеряется в метрах, дюймах или футах. Со своей стороны, относительная шероховатость — это отношение абсолютной шероховатости к диаметру трубы, поэтому она является безразмерной величиной. Относительная шероховатость важна, поскольку такая же абсолютная шероховатость более заметно влияет на тонкие трубы, чем на большие. Очевидно, что шероховатость труб взаимодействует с трением, которое, в свою очередь, снижает скорость, с которой жидкость движется внутри них. В очень длинных трубах жидкость может даже перестать двигаться. Поэтому очень важно оценить трение при анализе потока, поскольку для поддержания движения необходимо прикладывать давление с помощью насосов. Компенсация потерь требует увеличения мощности насосов, что сказывается на расходах. Другими источниками потери давления являются вязкость жидкости, диаметр трубы, ее длина, возможные сужения и наличие клапанов, кранов и колен. Происхождение шероховатостиВнутренняя часть трубы никогда не бывает полностью гладкой и гладкой на микроскопическом уровне. Стены имеют неровности поверхности, которые сильно зависят от материала, из которого они сделаны. Кроме того, после эксплуатации шероховатость увеличивается из-за накипи и коррозии, вызванной химическими реакциями между материалом трубы и жидкостью. Это увеличение может составлять от 5 до 10 раз больше заводской шероховатости. Для коммерческих труб значение шероховатости указывается в метрах или футах, хотя, очевидно, они будут действительны для новых и чистых труб, потому что со временем шероховатость изменит свое заводское значение. Значения шероховатости для некоторых коммерческих материаловНиже приведены общепринятые значения абсолютной шероховатости промышленных труб: — Медь, латунь и свинец: 1,5 х 10 -6 м (5 х 10 -6 футов). — Чугун без покрытия: 2,4 x 10 -4 м (8 х 10 -4 футов). — Кованое железо: 4,6 х 10 -5 м (1,5 х 10 -4 футов). — Клепанная сталь: 1,8 х 10 -3 м (6 х 10 -3 футов). — Коммерческая сталь или сварная сталь: 4,6 x 10 -5 м (1,5 х 10 -4 футов). — Чугун с асфальтовым покрытием: 1,2 x 10 -4 м (4 х 10 -4 футов). — Пластик и стекло: 0,0 м (0,0 фута). Относительную шероховатость можно оценить, зная диаметр трубы, изготовленной из рассматриваемого материала. Если обозначить абсолютную шероховатость как а также а диаметр как D, относительная шероховатость выражается как: В приведенном выше уравнении используется цилиндрическая труба, но в противном случае величина, называемая гидравлический радиус, в котором диаметр заменен на четырехкратное значение. Определение абсолютной шероховатостиДля определения шероховатости труб были предложены различные эмпирические модели, учитывающие геометрические факторы, такие как форма неровностей в стенах и их распределение. Примерно в 1933 году немецкий инженер Й. Никурадсе, ученик Людвига Прандтля, покрыл трубы песчинками разного размера, известные диаметры которых и являются абсолютной шероховатостью. а также. Никурадзе работал с трубками, для которых значения e / D варьировались от 0,000985 до 0,0333, В этих хорошо контролируемых экспериментах шероховатости были распределены равномерно, что на практике не происходит. Однако эти значения а также они по-прежнему являются хорошим приближением для оценки влияния шероховатости на потери на трение. Шероховатость, указанная производителем трубы, фактически эквивалентна шероховатости, созданной искусственно, как это сделали Никурадсе и другие экспериментаторы. По этой причине его иногда называют эквивалентный песок (эквивалент песка). Ламинарный поток и турбулентный потокШероховатость трубы — очень важный фактор, который следует учитывать в зависимости от режима движения жидкости. Жидкости, для которых важна вязкость, могут двигаться в ламинарном режиме или в турбулентном режиме. В ламинарном потоке, при котором жидкость движется упорядоченно слоями, неровности на поверхности трубы имеют меньший вес и поэтому обычно не принимаются во внимание. В этом случае именно вязкость жидкости создает напряжения сдвига между слоями, вызывая потери энергии. Примерами ламинарного потока являются струя воды, выходящая из крана с низкой скоростью, дым, начинающий хлынуть из зажженной ароматической палочки, или начало струи чернил, впрыскиваемой в струю воды, как определено Осборном Рейнольдсом. в 1883 г. Вместо этого турбулентный поток менее упорядочен и более хаотичен. Это поток, в котором движение нерегулярно и не очень предсказуемо. Примером может служить дым от ароматической палочки, когда он перестает плавно двигаться и начинает образовывать серию нерегулярных струй, называемых турбулентностью. Безразмерный числовой параметр, называемый числом Рейнольдса Nр указывает, есть ли у жидкости тот или иной режим, по следующим критериям: Безр 4000 поток турбулентный. Для промежуточных значений режим считается переходным, а движение неустойчивым. Коэффициент тренияЭтот коэффициент позволяет найти потерю энергии из-за трения и зависит только от числа Рейнольдса для ламинарного потока, но в турбулентном потоке присутствует относительная шероховатость. да F — коэффициент трения, для его определения существует эмпирическое уравнение, называемое уравнением Коулбрука. Это зависит от относительной шероховатости и числа Рейнольдса, но разрешить его непросто, поскольку F не указано явно: Вот почему были созданы такие кривые, как диаграмма Муди, которые позволяют легко найти значение коэффициента трения для данного числа Рейнольдса и относительной шероховатости. Опытным путем были получены уравнения, которые действительно имеют F явно, что довольно близко к уравнению Колебрука. Старение трубСуществует эмпирическая формула для оценки увеличения абсолютной шероховатости в результате использования, зная значение заводской абсолютной шероховатости. а такжеили: куда а также это грубость после т прошедших лет, а α — коэффициент с единицей измерения м / год, дюйм / год или фут / год, называемый скорость ежегодного увеличения шероховатости. Первоначально вычитается для чугунных труб, но хорошо работает с другими типами труб из металла без покрытия. В них pH жидкости важен с точки зрения ее долговечности, поскольку щелочные воды значительно уменьшают поток. С другой стороны, трубы с покрытием или пластик, цемент и гладкий бетон не испытывают заметного увеличения шероховатости со временем. Ссылки
Олигодендроциты: характеристики, виды и функции 25 незабываемых фраз драматурга Хасинто Бенавенте Гидравлически гладкие и шероховатые трубы
Состояние стенок трубы в значительной мере влияет на поведение жидкости в турбулентном потоке. Так при ламинарном движении жидкость движется медленно и плавно, спокойно обтекая на своём пути незначительные препятствия. Возникающие при этом местные сопротивления настолько ничтожны, что их величиной можно пренебречь. В турбулентном же потоке такие малые препятствия служат источником вихревого движения жидкости, что приводит к возрастанию этих малых местных гидравлических сопротивлений, которыми мы в ламинарном потоке пренебрегли. Такими малыми препятствиями на стенке трубы являются её неровности. Абсолютная величина таких неровностей зависит от качества обработки трубы. В гидравлике эти неровности стенок трубы называются выступами шероховатости. Шероховатость характеризуется величиной и формой различных выступов и неровностей, имеющихся на стенках трубы (рис. 5.6).
Рис. 5.6. К понятию абсолютной шероховатости, гидравлически гладких и шероховатых труб В качестве основной характеристики шероховатости служит абсолютная шероховатость — В зависимости от того, как относятся размеры выступов шероховатости и толщина ламинарной пленки, все трубы могут быть при турбулентном режиме движения подразделены на три вида. 1) Гидравлически гладкие трубы — 2) Гидравлически шероховатые трубы — 3) В третьем случае, являющемся промежуточным между двумя вышеуказанными, абсолютная высота выступов шероховатости примерно равна толщине ламинарной пленки — d » D. В этом случае трубы относятся к переходной области сопротивления. Толщина ламинарной пленки определяется по формуле Итак, различают стенки гидравлически гладкие и шероховатые трубы. Такое разделение является условным, поскольку, как следует из формулы (5.7), толщина ламинарной пленки обратно пропорциональна числу Рейнольдса (или средней скорости). Таким образом, при движении вдоль одной и той же поверхности с неизменной высотой выступа шероховатости в зависимости от средней скорости (числа Рейнольдса) толщина ламинарной пленки может изменяться. При увеличении числа Рейнольдса толщина ламинарной пленки dуменьшается и стенка, бывшая гидравлически гладкой, может стать шероховатой, так как высота выступов шероховатости окажется больше толщины ламинарной пленки и шероховатость станет влиять на характер движения и, следовательно, на потери напора. Для практических расчетов можно принимать ориентировочные значения высоты выступа шероховатости для труб: трубы новые стальные и чугунные — Δ ≈ 0,45 — 0,50 мм, трубы, бывшие в эксплуатации (так называемые «нормальные»), Δ ≈ 1,35 мм. Таким образом, зная высоту выступа шероховатости и определив толщину ламинарной пленки, можно определить гидравлически гладкой или гидравлически шероховатой будет стенка, ограничивающая поток в трубе. Технические характеристики полиэтиленовой трубы: плюсы и минусы в цифрахВиды шероховатостей в гидравликеТечение жидкости в ламинарном режиме происходит медленно и плавно, и она спокойно обтекает на своем пути небольшие препятствия. Местное сопротивление в этом случае настолько незначительное, что его величиной можно пренебречь.
При турбулентном потоке даже мелкие препятствия могут стать источником вихревого движения жидкостей. Они приводят к возрастанию точечных гидравлических сопротивлений, которые в ламинарном потоке настолько малы, что не заслуживают внимания. Препятствиями в данном случае считаются царапины, заусеницы, бугорки и т.п. на стенках трубопровода. В гидравлике они называются выступами шероховатости. Проблема данного вида может быть абсолютной или относительной:
Помимо двух основных видов существует также понятие эквивалентной шероховатости стальных труб, которая искусственно создается бугорками одинаковой высоты по всей длине трубопровода. При ее определении диаметр зерен подбирается так, чтобы в местах квадратичного сопротивления коэффициент по величине был равен коэффициенту при естественной неровности внутренней поверхности сетей.
Как найти шероховатость трубВ этой статье мы решим задачку на потерю напора в трубопроводе. Данная статья поможет вам понять, как идет сопротивление движению потока. На реальных цифрах, опишу алгоритм как это делать. Используем основные формулы. Разберем простой пример с трубой, как видно на изображении в начале трубы насос потом идет манометр, который позволяет измерить давление жидкости в начале трубы. Через определенную длину установлен второй манометр, который позволяет измерить давление в конце трубы. Ну и в самом конце стоит кран. Эта схема достаточно проста, и я попытаюсь привести примеры. И так начнем. Вообще существует не один способ как узнать потерю напора: Способ, когда известно давление вначале и в конце трубы, можно вычислить потерю напора по формуле: М1-М2=Давление , то есть эта разница между двумя манометрами. Допустим у нас получилось, грубо говоря 0,1 МПа, что составляет одну атмосферу. Это значит у нас потеря напора по длине составляет 0,1 МПа. Обратите внимание, мы можем указывать потерю напора по двум величинам, это по гидростатическому давлению, что составляет 0,1 МПа и по высоте напора водного столба в метрах, что составляет 10 метров. Как я не однократно говорил каждые 10 метров это одна атмосфера давления. Существует ряд методов, как рассчитать потерю напора не имея манометров на трубах. Ученые исследователи приготовили для нашего пользования замечательные формулы и цифры, которые нам пригодятся. Существует хорошая формула которая позволяет вычислить потерю напора по длине трубопровода.
А теперь поговорим о коэффициенте гидравлического трения. Формулы нахождения этого коэффициента зависит от числа Рейнольдса и эквивалента шероховатости труб. Напомню эту формулу (она применима только к круглым трубам):
Далее находим формулу для нахождения коэффициента гидравлического трения по таблице:
— Эквивалент шероховатости труб. Эта величина в таблицах указывается в милиметрах, но вы когда будете вставлять в формулу обязательно переводите в метры. Вообще не забывайте соблюдать пропорциональность единиц измерения и не смешивайте в формулах разных типа [мм] с [м]. d-внутренний диаметр трубы, то есть диаметр потока жидкости. Также хочу подметить, что подобные величины по шероховатости бывают абсолютными и относительными или даже есть относительные коэффициенты. Поэтому когда если будете искать таблицы с величинами, то величина эта должа называться «эквивалентом шероховатости труб» и не как иначе, а то результат будет ошибочный. Эквивалент означает — средняя высота шероховатости. В некоторых ячейках таблицы указаны две формулы, вы можете считать на любой выбранной, они почти дают одинаковый результат. Таблица: (Эквивалент шероховатости)
Таблица: (Кинематическая вязкость воды
А теперь давайте решим задачу: Найти потерю напора по длине при движении воды по чугунной новой трубе D=500мм при расходе Q=2 м 3 /с, длина трубы L=900м, температура t=16°С.
МатериалВ наибольшей степени свойства любого предмета определяются тем, из чего он сделан. Полиэтиленовые трубы не исключение.
Полиэтиленовые трубы не боятся ни света, ни непогоды А сделаны они из материала, который является самым распространенным из существующих пластиков. Его физические свойства таковы:
Насколько было бы чище вокруг, если бы весь полиэтилен разлагался за год…
ЧИТАТЬ ТАКЖЕ: Можно ли полипропиленовые трубы прятать в стену – вопросы мастеру, Портал о трубах
Полиэтилену это не грозит
Кроме того, на время зимнего отсутствия воду из труб желательно сбросить еще по одной причине: трубам лед не страшен, а вот смесители он порвет. h м = ζ v 2 /2g.
При развитом турбулентном режиме ζ = const, что позволяет ввести в расчеты понятие эквивалентной длины местного сопротивления Lэкв. т.е. такой длины прямого трубопровода, для которого ht = hм. В данном случае потери напора в местных сопротивлениях учитываются тем, что к фактической длине трубопровода добавляется сумма их эквивалентных длин
Зависимость потерь напора h1-2 от расхода называется характеристикой трубопровода. В случаях когда движение жидкости в трубопроводе обеспечивает центробежный насос, то для определения расхода в системе насос – трубопровод выстраивается характеристика трубопровода h =h(Q) с учетом разности отметок ∆z (h1-2 + ∆z при z1 z2) накладывается на напорную характеристику насоса H=H(Q), которая приведена в паспортных данных насоса (смотреть рисунок). Точка пересечения таких кривых указывает на максимально возможный расход в системе. Adblock detector Для любых предложений по сайту: e-polirovka@cp9.ru |

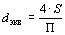 ,
,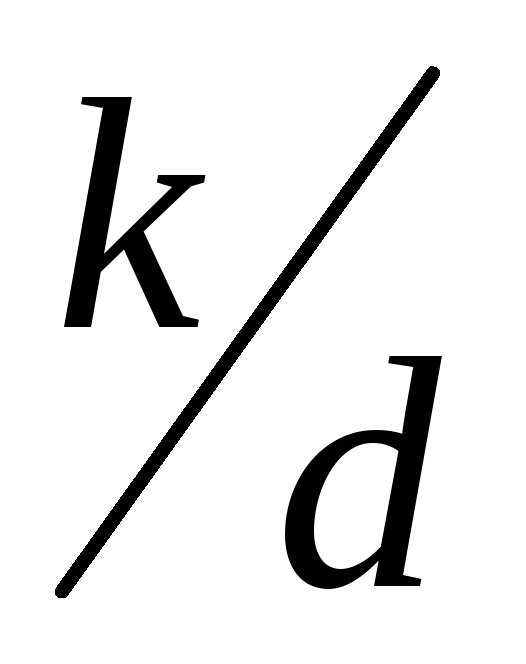 .
.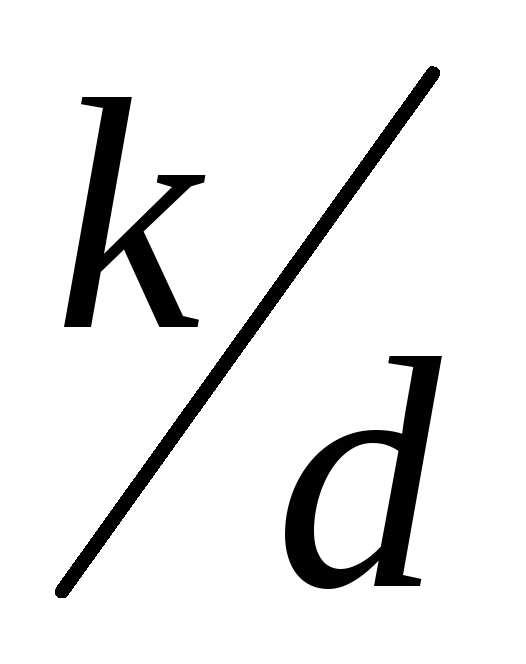 .
. . В общем случае коэффициент гидравлического трения может зависеть от двух безразмерных параметров – числа
. В общем случае коэффициент гидравлического трения может зависеть от двух безразмерных параметров – числа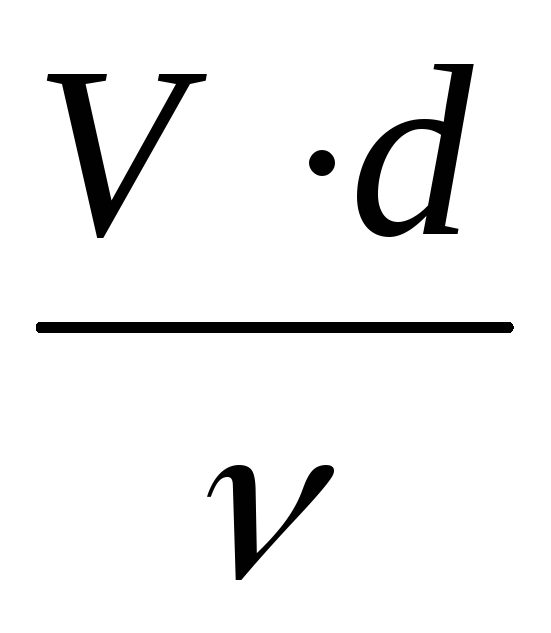 и k/d, т.е.
и k/d, т.е. 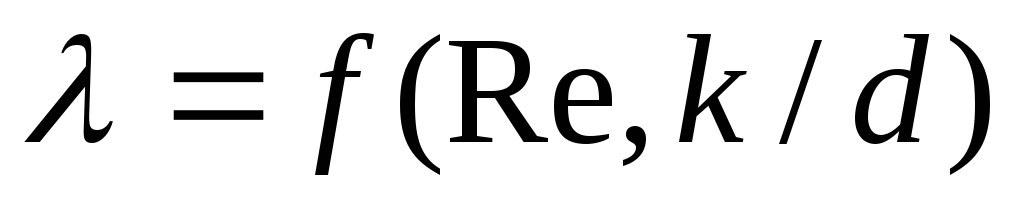 .
. от числа Рейнольдса, на нем изменение коэффициента
от числа Рейнольдса, на нем изменение коэффициента представлено рядом кривых, каждая из которых соответствует определённой относительной шероховатости, т.е. отношениюk/d.
представлено рядом кривых, каждая из которых соответствует определённой относительной шероховатости, т.е. отношениюk/d. зависит от числа Рейнольдса, в доквадратичной области коэффициент
зависит от числа Рейнольдса, в доквадратичной области коэффициент зависит от числаRe и от относительной шероховатости, а в области квадратичного сопротивления – только от относительной шероховатости.
зависит от числаRe и от относительной шероховатости, а в области квадратичного сопротивления – только от относительной шероховатости.
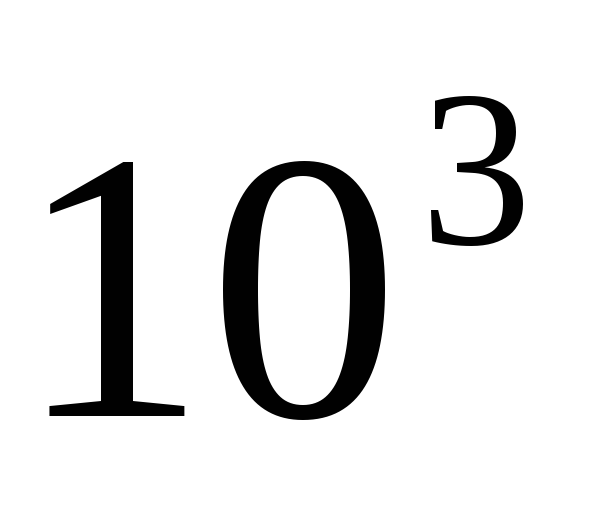
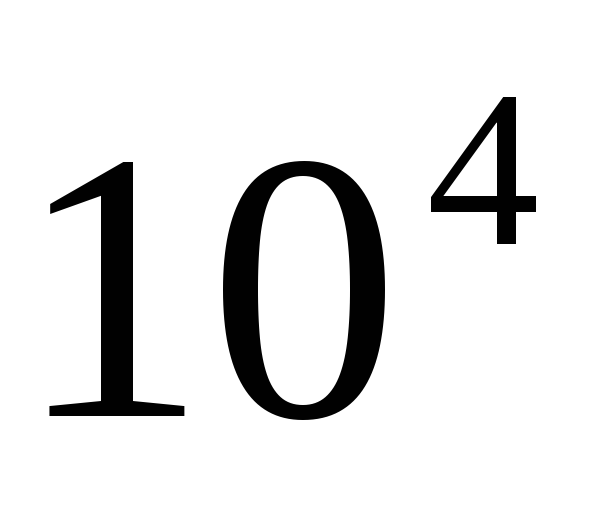
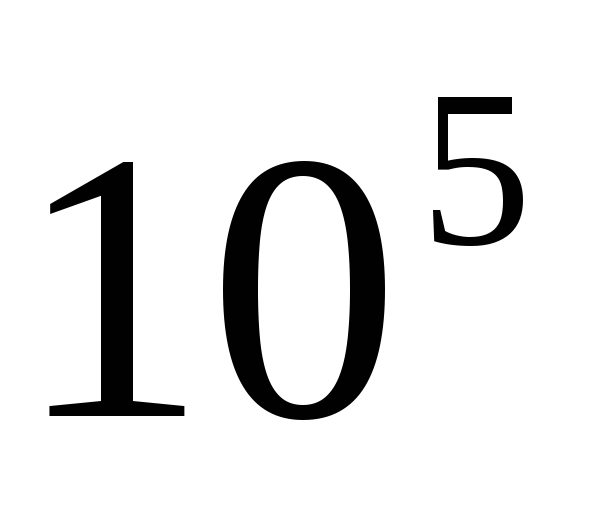
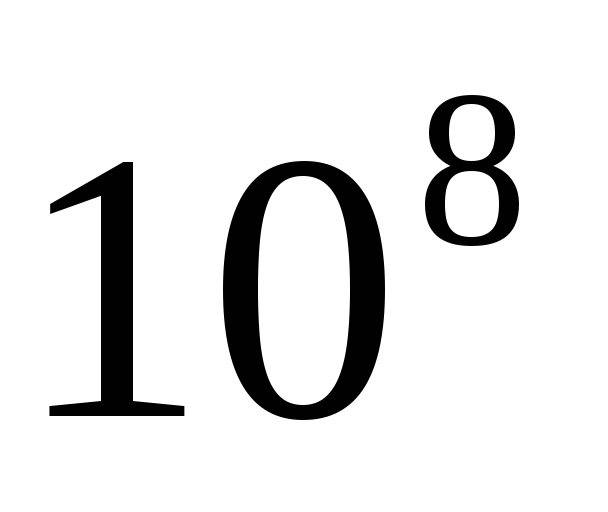
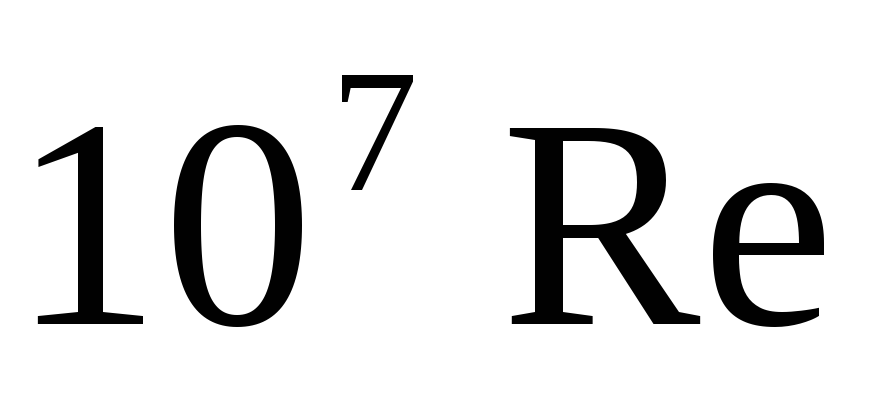
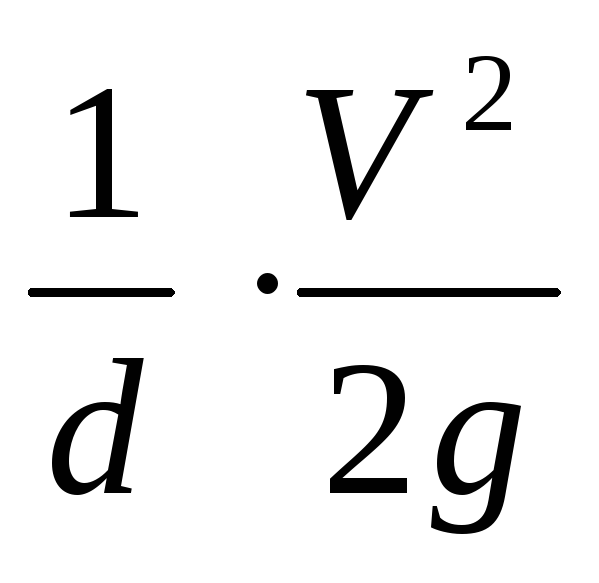 .
.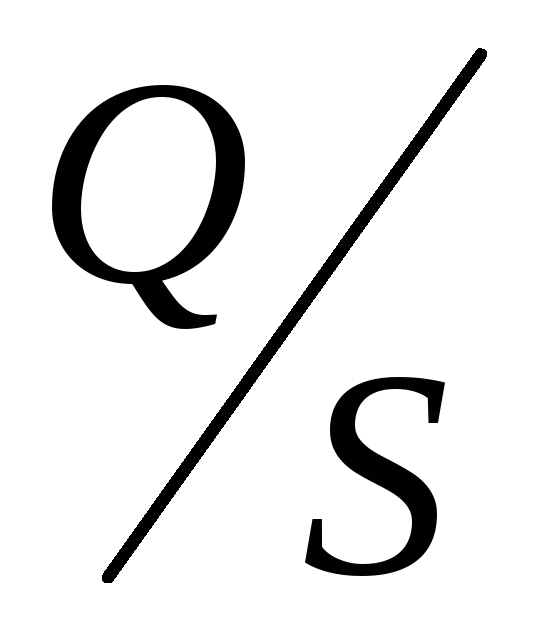 =
=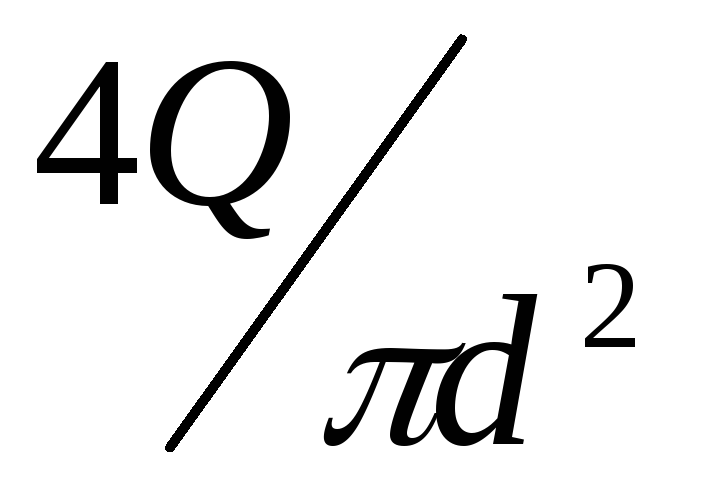 ;
;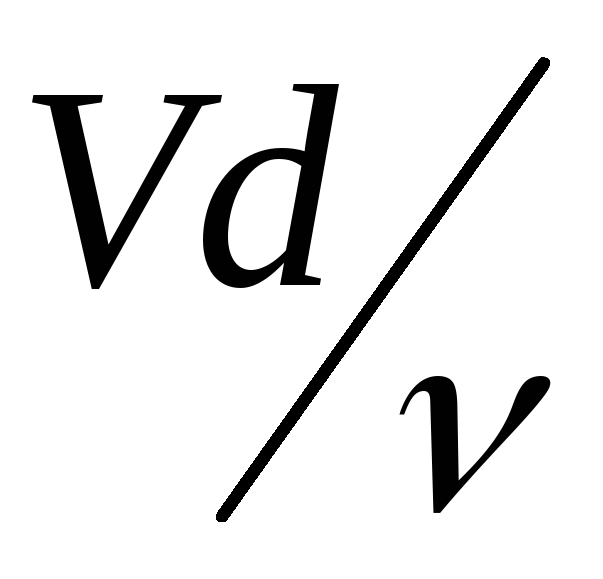 ;
;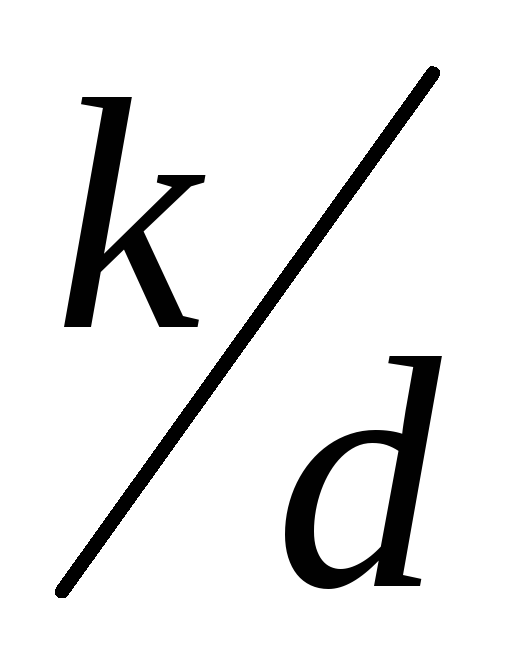 .
.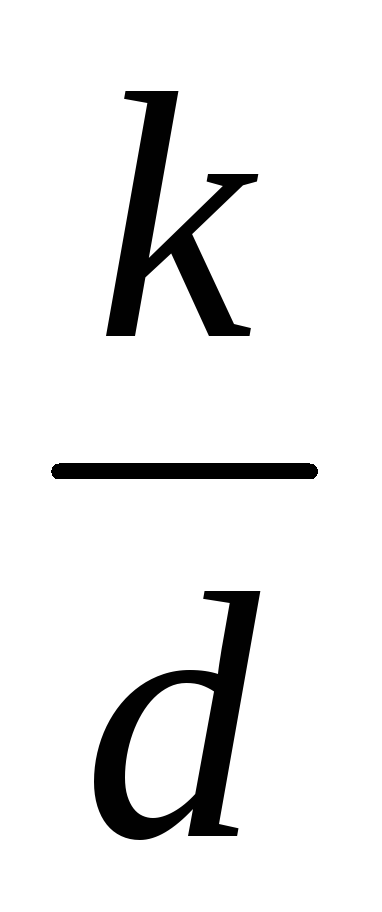 .
.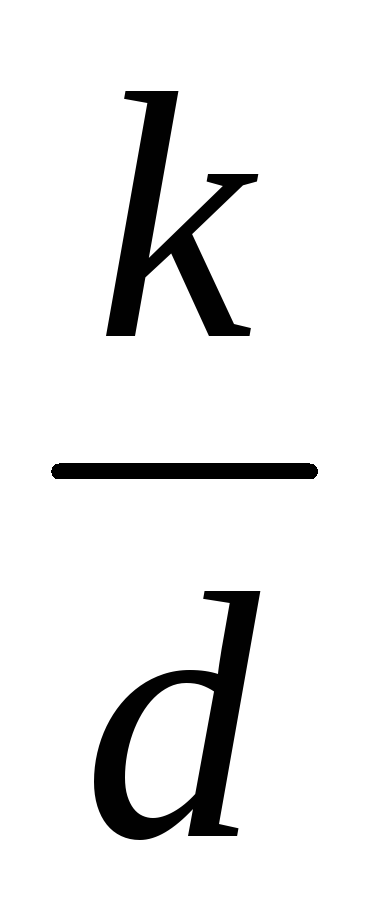 500, то имеет место квадратичная зона сопротивления и λ определяется по формуле Шифринсона
500, то имеет место квадратичная зона сопротивления и λ определяется по формуле Шифринсона . (10.4)
. (10.4) в соответствующей зоне сопротивления.
в соответствующей зоне сопротивления.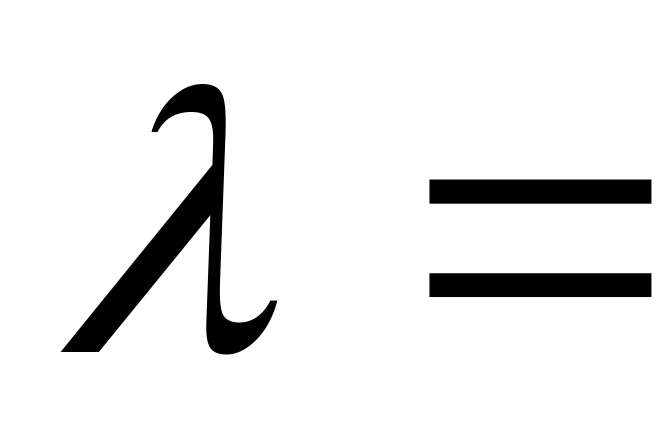 64/Rе и потери hl выразятся так
64/Rе и потери hl выразятся так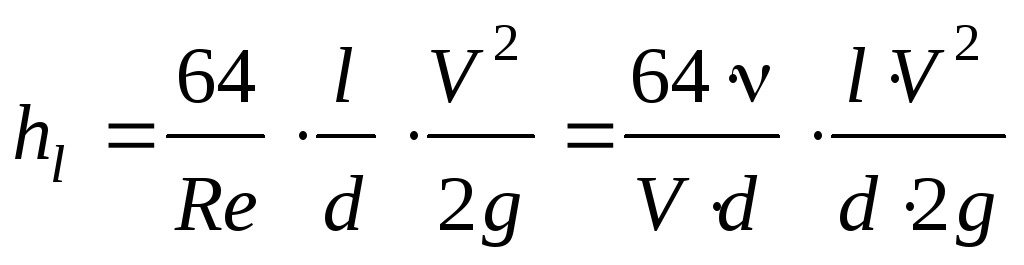 или, сокращая числитель и знаменатель на V,
или, сокращая числитель и знаменатель на V, 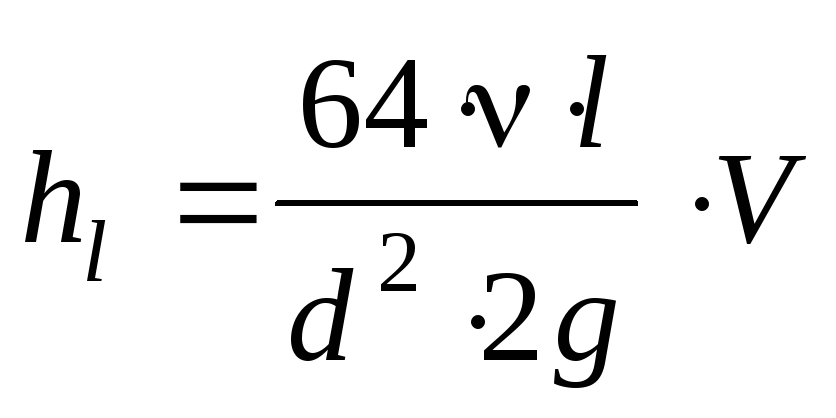 .
.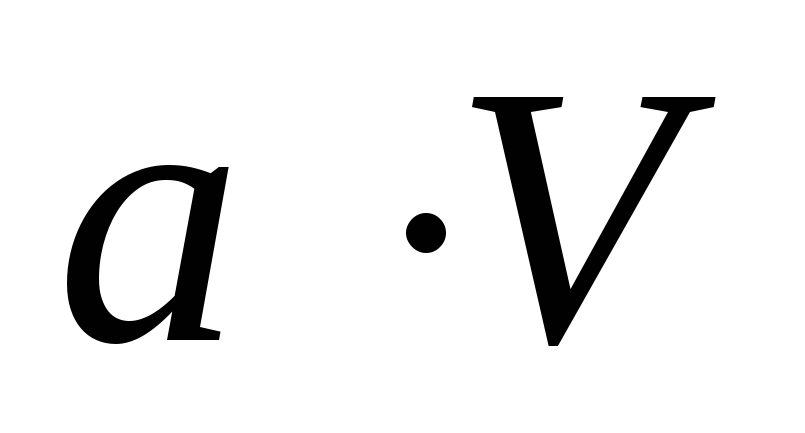 , т.е. потери в ламинарной зоне сопротивления пропорциональны первой степени скорости.
, т.е. потери в ламинарной зоне сопротивления пропорциональны первой степени скорости.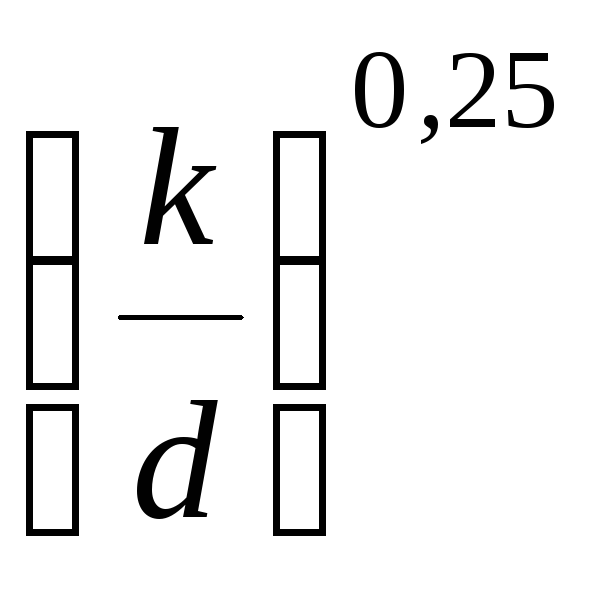 , а потери выразятся так hl=0,11
, а потери выразятся так hl=0,11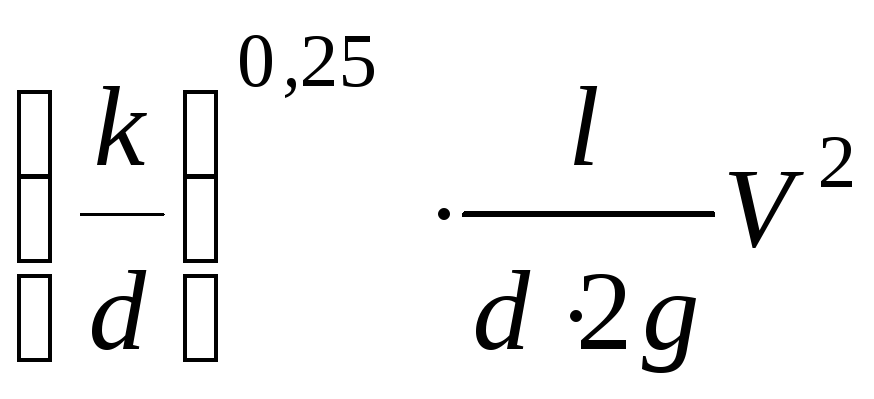 .
.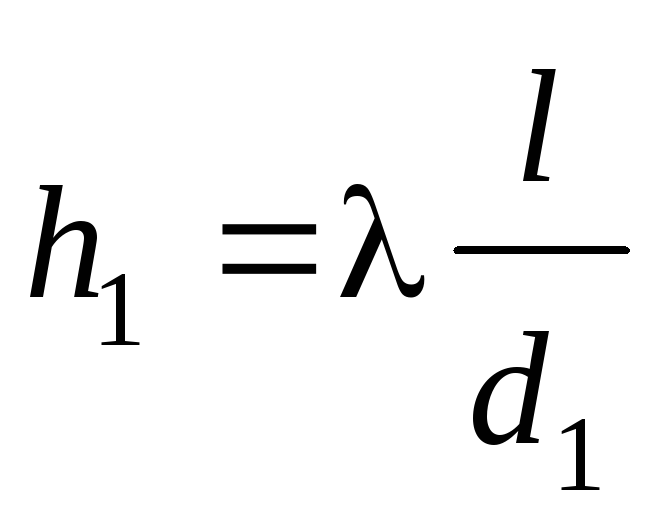
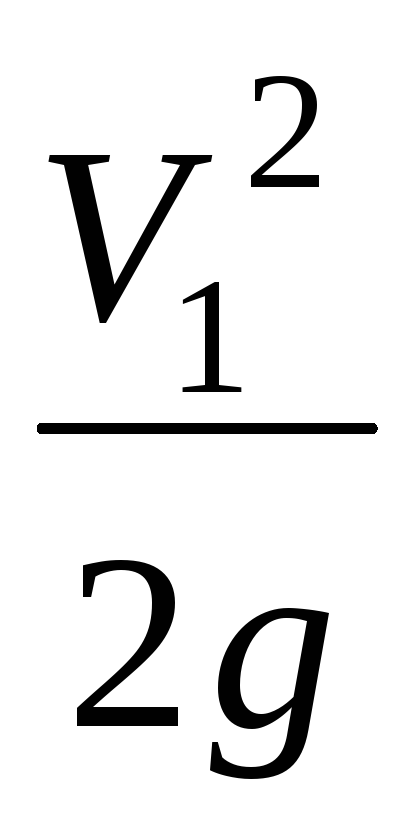 и
и 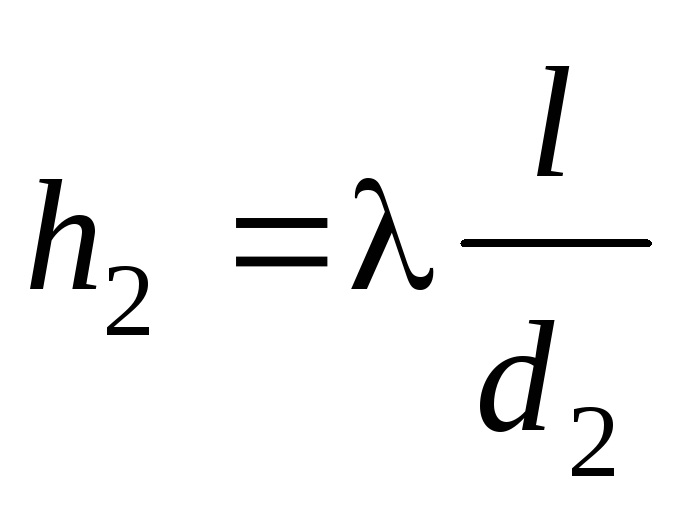
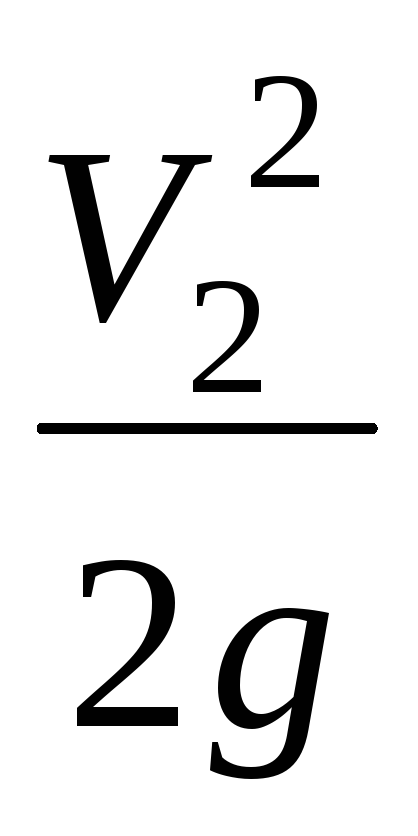 . Их отношение
. Их отношение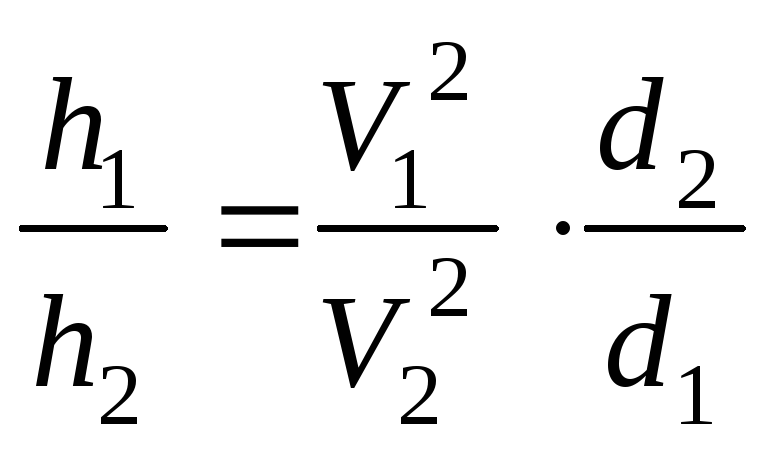 .(10.5)
.(10.5)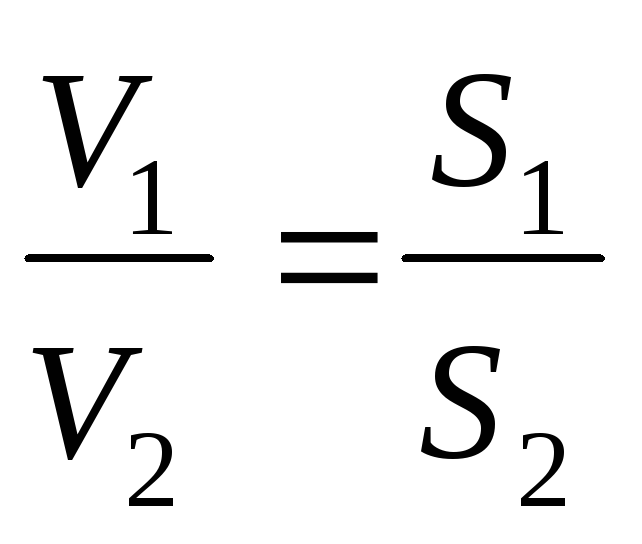 или
или 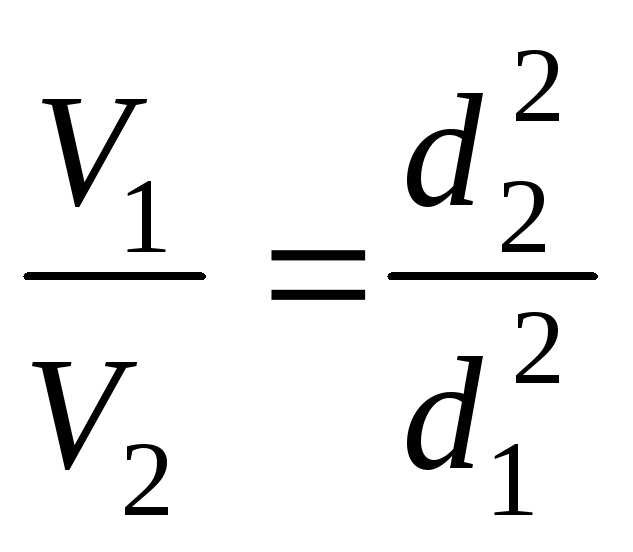 .
. . (10.6)
. (10.6)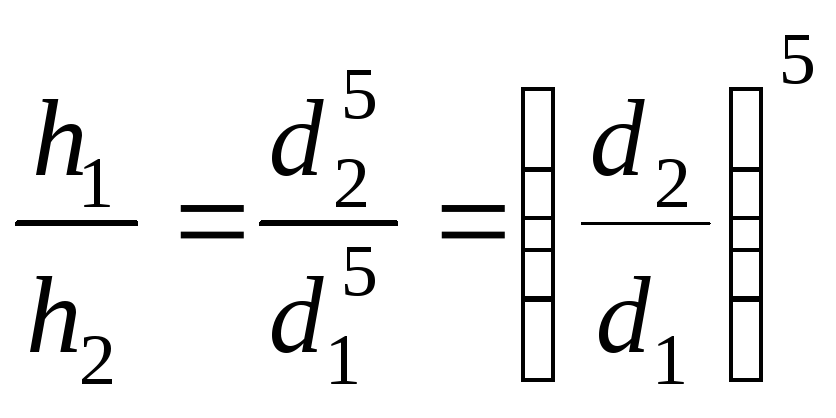 .
.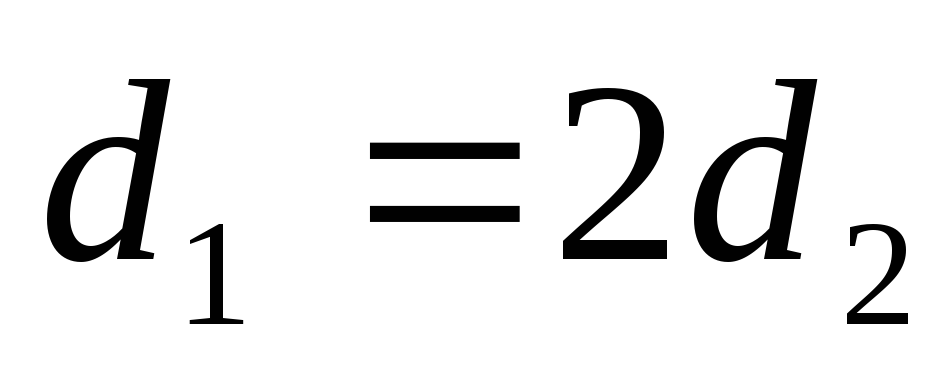 , то
, то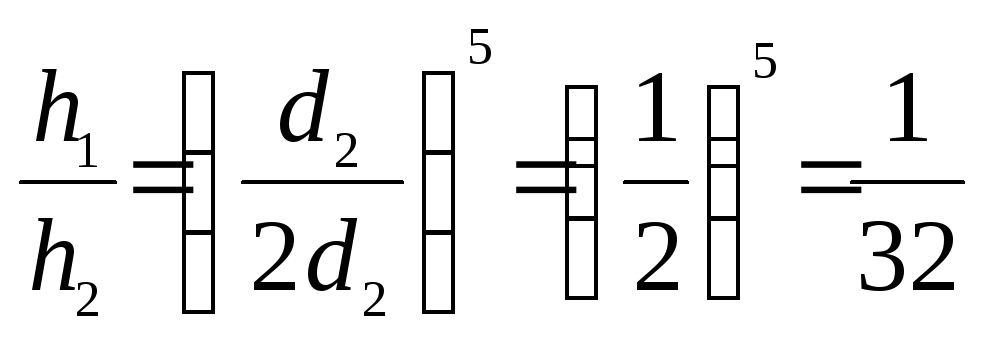 .
. также зависит от диаметра, то получим несколько меньшее число.
также зависит от диаметра, то получим несколько меньшее число.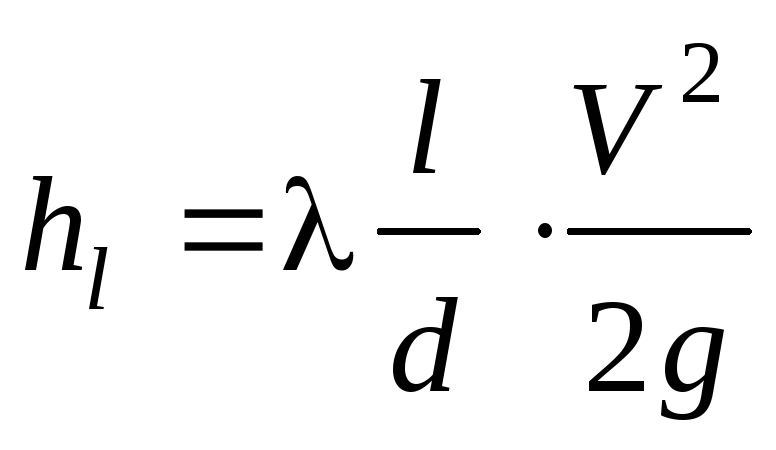 или
или 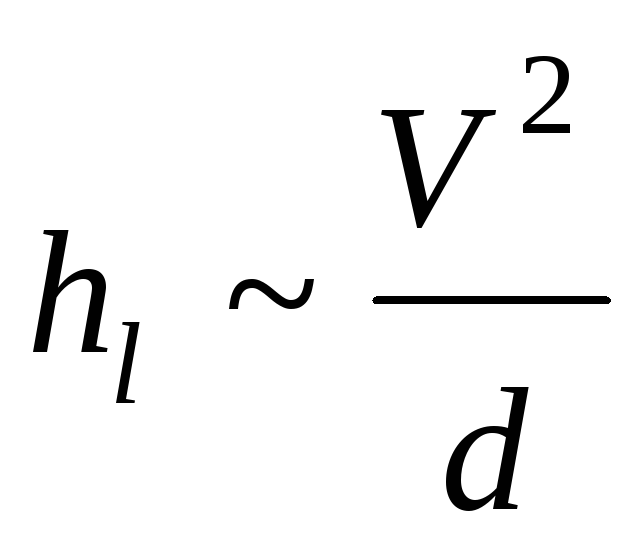 .(10.7)
.(10.7) обратно пропорциональна квадрату диаметра, а средняя скорость в квадрате, соответственно, обратно пропорциональна четвертой степени диаметра, т.е.
обратно пропорциональна квадрату диаметра, а средняя скорость в квадрате, соответственно, обратно пропорциональна четвертой степени диаметра, т.е.





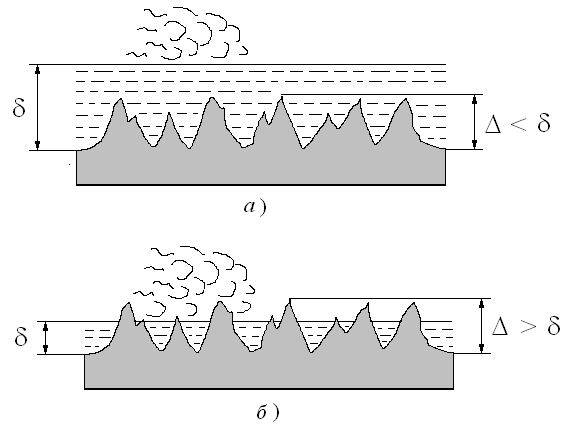
 , которая равна средней высоте бугорков шероховатости. Отношение абсолютной шероховатости
, которая равна средней высоте бугорков шероховатости. Отношение абсолютной шероховатости 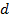 называется относительной шероховатостью —
называется относительной шероховатостью —  .
.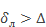 , т.е. толщина ламинарного слоя больше высоты выступов шероховатости. В этом случае шероховатость стенок не влияет на характер движения и соответственно потери напора не зависят от шероховатости.
, т.е. толщина ламинарного слоя больше высоты выступов шероховатости. В этом случае шероховатость стенок не влияет на характер движения и соответственно потери напора не зависят от шероховатости.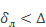 , т.е. толщина ламинарного слоя меньше высоты выступов шероховатости. В этом случае шероховатость стенок влияет на характер движения и соответственно потери напора зависят от шероховатости.
, т.е. толщина ламинарного слоя меньше высоты выступов шероховатости. В этом случае шероховатость стенок влияет на характер движения и соответственно потери напора зависят от шероховатости.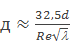 . (5.7)
. (5.7)