Модуль сдвига стали при кручении
Испытание образца на кручение с определением модуля сдвига
В методических указаниях к лабораторной работе N 4 » Испытание образца на кручение с определением модуля сдвига» указывается цель работы, приводится характеристика испытуемого образца и дается методика проведения испытаний. Для лучшего усвоения материала по теме «Кручение» приводятся основные теоретические положения, позволяющие квалифицированно провести испытания, определить величину модуля сдвига и проанализировать полученные результаты испытания.
Завершаются методические указания перечнем возможных вопросов при защите отчета по этой лабораторной работе.
Определить опытным путем величину модуля сдвига (G), сравнить полученное значение со справочным для данного материала и проверить справедливость закона Гука при данном испытании.
3. ОБОРУДОВАНИЕ, ПРИБОРЫ И ИНСТРУМЕНТЫ
Испытательная машина – КМ-50 Индикатор часового типа Штангенциркуль Мерительная линейка.
4. ХАРАКТЕРИСТИКА ОБРАЗЦА
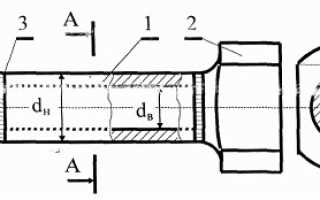
Вид испытуемого образца представлен на рис.1. Головки образца, предназначенные для крепления в захватах машины KiVI-50, изготовлены из сплошного материала и присоединены к телу образца с помощью сварки. На головках образца имеются лыски, исключающие прокручивание их в захватах машины. Материал образца – сталь ст.З.

Рис.1. Вид испытуемого образца:
1 – тело образца,
2 – головка образца,
5. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
При сдвиге в упругой стадии (рис. 2) справедлив закон Гука, который устанавливает прямую пропорциональную зависимость между касательным напряжением (τ) и углом сдвига (γ):
Величина G представляет собой коэффициент пропорциональности и называется модулем упругости второго рода или модулем сдвига. Закон Гука справедлив при напряжениях не
превышающих предел пропорциональности – Тпц.

Рис. 2. Деформация сдвига
При кручении стержня круглого сечения его элементы находятся в состоянии чистого сдвига (рис.3).
Учитывая, что при кручении напряжения – τ зависят от крутящего момента Μ , а угол закручивания – φ от угла сдвига – γ, то получим выражение закона Гука при кручении:
 (1)
(1)
где: γ – угол закручивания, радиан
Mk – крутящий момент, Η м
I – длина образца, м
G – модуль сдвига. Па
Jp – полярный момент инерции (м4), который для полого вала равен:
 (2)
(2)
где: dH – наружный диаметр
dB – внутренний диаметр сечения.

Рис.3. Напряжения и деформации при кручении
При известных значениях i и Jp можно, измерив крутящий момент Мк и соответствующий угол закручивания посчитать величину модуля сдвига G , выразив его из формулы (1):
%  (3)
(3)
Угол закручивания (φ) определяется с помощью приспособления, закрепленного на теле образца (рис.4).
Приспособление для измерения угла закручивания состоит из двух рычагов 3 и 4 жестко закрепленных на образце 1 на расстоянии i друг от друга. На рычаге 3 укреплен индикатор часового типа 2, измерительный наконечник которого контактирует с рычагом 4. При закручивании образца происходит взаимное перемещение (Δ) концов обоих рычагов, которое измеряется с помощью индикатора 2 (рис.5). Угол закручивания образца (Δφ= tgAcp , ввиду малости этого угла ) равен:
 (4)
(4)
где: Δ – взаимное смещение концов рычагов 3 и 4, измеряемое индикатором 2;
Ки – расстояние от оси образца до измерительного наконечника индикатора, показанное на рис.5 (Ки = гн + а).

Рис.4. Образец с приспособлением для измерения угла закручивания
6. ПОРЯДОК ПРОВЕДЕНИЯ ИСПЫТАНИЙ
1. Перед испытанием студентам необходимо ознакомиться с устройством машины КМ-50 (первое занятие) и правилами поведения в лаборатории при проведении испытаний (вводный инструктаж).

Рис.5. Схема измерения угла закручивания
2. Измеряют штангенциркулем характерные линейные размеры испытуемого образца, расстояния между обоймами приспособления для измерения угла закручивания и от образующей образца до центра наконечника индикатора часового типа («а» на рис.5 ).
3. Приступая к испытанию необходимо дать предварительную небольшую нагрузку для устранения зазоров и обжатия образца, и провести первые отсчеты по приборам (силоизмерителю и индикатору), лучше, если можно, приборы установить
4. Вручную производят статическое нагружение образца крутящим моментом равными ступенями ΔΜΚ . Нагружение следует производить плавно, без рывков рукоятки.
5. После каждого увеличения крутящего момента на величину ΔΜΚ снимают отсчет по индикатору (число делений индикатора). Запись отсчетов производят в таблицу, графы 1 и 3.

6. В процессе проведения испытаний внимательно следят за комментариями преподавателя и при завершении испытаний по его указанию приступают к обработке результатов испытания.
7. ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЯ
Обработка результатов испытания производится с помощью таблицы. На каждой ступени приращения момента ΔΜΚ определяют приращения отсчетов по индикатору ΔΑ , вычитая из показания индикатора А на каждом этапе нагружения показания его на предыдущем этапе нагружения. Полученные результаты ΔΑ записывают в графу 4.
Угол закручивания ( в минутах ) для каждого значения крутящего момента (графа 1 ) определяется по формуле:

Полученные значения угла закручивания заносятся в графу 5 .
Среднее приращение отсчетов АсрА определяется суммированием приращений отсчетов ΔΑ (графа 4) с последующим делением на количество приращений отсчетов:

где η – количество приращений отсчетов.
Средний угол закручивания (в радианах) определяется делением среднего приращения отсчетов А на радиус R
 (5)
(5)
Модуль сдвига G определяется по формуле ( 3 ) с учетом того что мы берем не полные углы закручивания, а средние их приращения, т.е.:
где: t – расчетная длина (расстояние между точками крепления обойм приспособления для измерения угла закручивания на испытуемом образце);
Jp – полярный момент инерции сечения образца, определяется по формуле (2);
Мк – среднее приращение крутящего момента; Лсрф – средний угол закручивания ( в радианах ) на базовой
длине , определяется по формуле (5).
Для проверки справедливости закона Гука при данном испытании строится график в координатах (φ – Мк). По оси абсцисс откладываются углы закручивания (q>j) , а по оси ординат – соответствующие им крутящие моменты (М-,- )· Полученные точки соединяют между собой отрезками прямых. В идеальном случае точки диаграммы должны лежать на одной прямой. Чем дальше от прямой отстоят эти точки, тем хуже материал образца подчиняется закону Гука. Существует связь между модулем упругости первого рода ( Ε), модулем упругости второго рода ( G ) и коэффициентом Пуассона (μ ):
Поэтому при анализе полученных результатов испытания и последующих выводах нужно воспользоваться ранее полученными значениями для Ε и μ ( лабораторная работа N 3 ), посчитать модуль сдвига G и сравнить его с найденным в данном испытании.
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА СТАЛИ ДИНАМИЧЕСКИМ МЕТОДОМ
КРАТКАЯ ТЕОРИЯ. Под влиянием внешних сил всякое тело изменяет свою форму и размеры, т.е. деформируется. Упругой называется деформация, исчезающая с прекращением действия силы. Существуют различные типы деформации: растяжение (сжатие), сдвиг, кручение.
 Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 1).
Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 1).
Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно. Так как угол мал, формулу можно записать в виде:
 (1)
(1)
где СС1=ΔX- абсолютный сдвиг, γ — угол сдвига, называемый также относительным сдвигом, выражается в радианах.
По закону Гука относительный сдвиг γ пропорционален касательному напряжению F/S, где S — площадь поверхности грани ВС, т.е.
 , (2)
, (2)
где N — модуль сдвига:
 . (3)
. (3)
Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном единице (при условии, что закон Гука выполняется).
Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ — угол кручения. По закону Гука:
 . (4)
. (4)
Модуль кручения f показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.
 В результате деформации кручения возникает перекос образующих цилиндрической поверхности стержня (рис. 2), причем
В результате деформации кручения возникает перекос образующих цилиндрической поверхности стержня (рис. 2), причем
 (5)
(5)
Поэтому расчет деформации кручения может быть сведен к расчету деформации сдвига. Приведем без вывода соотношение, существующее между модулем кручения f и модулем сдвига N материала проволоки
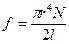 (6)
(6)
где r, l — соответственно радиус и длина проволоки. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки. Из формулы (6) имеем
 (7)
(7)
Таким образом, модуль сдвига материала можно найти, зная модуль кручения, радиус и длину проволоки.
 Динамический метод измерения модуля кручения основан на зависимости периода Т крутильных колебаний маятника, подвешенного на проволоке, от упругих свойств материала проволоки. Крутильным маятником служит рейка К с надетыми на нее цилиндрическими грузами Р, подвешенная на проволоке длиной L,радиусом r (см. рис. 3).
Динамический метод измерения модуля кручения основан на зависимости периода Т крутильных колебаний маятника, подвешенного на проволоке, от упругих свойств материала проволоки. Крутильным маятником служит рейка К с надетыми на нее цилиндрическими грузами Р, подвешенная на проволоке длиной L,радиусом r (см. рис. 3).
Если колеблющиеся тела совершают вращательное движение, то к ним может быть применен основной закон динамики вращательного движения:
 (8)
(8)
где М — вращающий момент относительно оси АВ, J — момент инерции тела относительно той же оси,  — угловое ускорение.
— угловое ускорение.
Учитывая (4) и (8) можно переписать в виде:
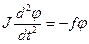 (9)
(9)
Знак минус говорит о том, что вращающий момент сдвига направлен так, чтобы уменьшить угловое отклонение.
Таким образом, тело совершает гармонические колебания, периоды которых можно найти из условия, что множитель пропорциональности между  и φ в уравнении (9) в данном случае 1/J должен быть равен:
и φ в уравнении (9) в данном случае 1/J должен быть равен:
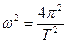 , т.е.
, т.е. 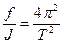 .
.
 , (10)
, (10)
где Т — период колебания маятника.
Чтобы найти f, необходимо исключить неизвестный момент инерции J. Для этого в задаче определяются два периода колебаний маятника. Используя возможность передвижения груза Р на рейке установки, меняем расстояние от оси вращения. В соответствии с l1 и l2 получаем моменты инерции J1 и J2.
 ,
,  , (11)
, (11)
где J — момент инерции рейки крутильного маятника. Периоды колебаний будут соответственно равны:
 , Þ
, Þ  . (12)
. (12)
 Решая совместно два последних уравнения, получим формулу для расчета модуля кручения проволоки крутильного маятника:
Решая совместно два последних уравнения, получим формулу для расчета модуля кручения проволоки крутильного маятника:
 . (13)
. (13)
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА изображена на рис. 4. Крутильный маятник представляет собой стальной цилиндр Ц с двумя стержнями С, подвешенный с помощью двух стальных проволок к неподвижному кронштейну К. Момент инерции маятника J можно изменять перемещая вдоль стержней одинаковые стальные цилиндры m.
1. Измерить L1, L2 и радиус проволоки r.
2. Снять зависимость Т периода полного колебания крутильного маятника от  момента инерции измеряя время t 50 полных колебаний.
момента инерции измеряя время t 50 полных колебаний.
3. Результаты эксперимента занести в таблицу.
| i, j |
 , мм , мм |
| t, с |
| T, с |
4. Используя соотношения:
 ,
,  кг/м 3 , m=0,64 кг,
кг/м 3 , m=0,64 кг,  =3,4,
=3,4, 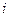 =1.2, вычислить Nji. Оценить погрешность измерения модуля сдвига стали.
=1.2, вычислить Nji. Оценить погрешность измерения модуля сдвига стали.
5.Результаты вычислений занести в таблицу.
| j,i | N,10 10 Н/м 2 | Nср,10 10 Н/м 2 | ΔN,10 10 Н/м 2 | ΔNср,10 10 Н/м 2 |
| 3, 1 | ||||
| 3, 2 | ||||
| 4, 1 | ||||
| 4, 2 |
6.Результат эксперимента представить в виде
 Н/м 2 .
Н/м 2 .
Определение модуля сдвига и кручения статическим методом

Определение модуля сдвига и кручения статическим методом.
Теоретическое введение
Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то угол кручения по закону Гука оказывается равным φ = СМ, где С — коэффициент, зависящий от вещества проволоки. Модуль кручения f, равный
f=l/C=M/ φ (1)
показывает, какой момент сил нужно приложить, чтобы закрутить проволоку на угол в один радиан.
Модуль сдвига G равен:
G=P/(Sw)=τ /w (2)
где P/S определяет величину касательного усилия на единицу поверхности, a w — угол сдвига (рис. 1), — касательное напряжение на грани кубика.

Между модулем кручения f и модулем сдвига материала стержня существует простая связь; найдем ее, рассматривая деформации и усилия, возникающие при закручивании стержня.
Пусть стержень диаметром D = 2r и длиной L из материала, модуль сдвига которого равен G, закручен действием момента сил МЗ, на угол φo, это значит, что основания его повернулись на угол φо относительно друг друга.
Прежде всего отметим, что в любом сечении стержня, перпендикулярном к оси, момент внутренних усилий относительно оси стержня равен МЗ моменту сил, закручивающих стержень. Действительно, представим себе мысленно отрезанной какую-то часть В закрученного стержня (рис. 2, а). Так как часть В находится в покое, то моменты всех сил, действующих на нее, равны нулю. С одного конца на эту часть действует момент внешних сил МЗ, а с другого — момент внутренних усилий M касательных к сечению; величин равна M  равна МЗ, и противоположна по знаку.
равна МЗ, и противоположна по знаку.

Далее определим, как распределены касательные напряжения в сечении стержня и как они связаны с деформацией. Вырежем из стержня диск достаточно малой высоты ∆I на расстоянии I от неподвижного основания и предположим, что нижнее основание этого диска при закручивании повернулось на угол φ , а верхнее на угол φ + ∆φ . Из этого диска вырежем кольцо с внутренним радиусом г и внешним r+∆r (рис. 2,б) Тогда все кубики, вырезанные из кольца, будут иметь одинаковую деформацию сдвига, на один и тот же угол ∆α . Так как верхнее основание диска поворачивается относительно нижнего на малый угол ∆φ , не деформируясь, то очевидно, что угол сдвига ∆α. будет пропорционален радиусу кольца г. Смещение верхней поверхности кольца относительно нижнего будет равно:
∆α = ∆r∆α = r∆φ .
Поэтому угол сдвига
∆α = r∆φ/∆I
или угол сдвига кольца равен радиусу кольца, умноженному на производную от угла закручивания стержня по его длине ∆φ /∆I.
Теперь определим касательное усилие на поверхности кольца площадью 2πr∆r, напряжение t по формуле (2) равно:
t = G ∆α = G r ∆φ /∆ ,
,
поэтому усилие на поверхности кольца составляет:
2r∆r = 2π r2G∆φ r/∆I
Момент этого усилия относительно оси стержня равен:
∆M = 2πr2G∆φ ∆r/∆I.
Теперь соберем моменты усилий по поверхности диска и проинтегрируем это уравнение по r:
M = 2πG∆φ/ φ I = π r G∆φ/2∆I (3)
G∆φ/2∆I (3)
Этот момент должен быть равен моменту, закручивающему стержень МЗ, ибо моменты, приложенные к любым двум прилежащим дискам, равны друг другу. Уравнение (3) показывает, что если стержень однороден, то производная угла закручивания стержня ∆φ /∆I постоянна вдоль стержня. Угол закручивания торцевых сечений стержня, находящихся на расстоянии Iо , равен:
φo= Io∆φ/∆I или ∆φ/∆I = φo/Io
Подставив это выражение в формулу (3), получим зависимость угла закручивания стержня φo от закручивающего момента MЗ, в следующем виде:
MЗ = MO = π rc4Gφo /2I. (4)
Таким образом, сравнивая (4) с (1), находим, что модуль кручения f равен:
f= M rC G / I. (5)
Отметим, что размерность модулей упругости на растяжение Е и изгиб G одна и та же. В самом деле, размерность модуля Е:
[E]=[Pa /S∆L] =[P/S],
а размерность модуля сдвига:
[G]=[P/SW]=[P/S].
Числовая величина модулей упругости зависит, таким образом, от единиц, в которых измерена сила и площадь. В системе СГС модули упругости выражаются в дин/см2, в практической системе в кг/мм2 и в системе СИ в Н/м2.
Если желают перейти от значения модуля в практической системе к значению модуля в СГС, то, очевидно, значение модуля в практической системе нужно умножить на 9,82*107.
Измерение модуля кручения может быть выполнено статическим методом. В этом случае измеряется угол закручивания проволоки под действием определенного закручивающего момента.
Описание прибора
 К нижнему концу стержня АВ, закрепленного в кронштейне С, прикреплен металлический диск D (рис.3).
К нижнему концу стержня АВ, закрепленного в кронштейне С, прикреплен металлический диск D (рис.3).
По окружности диска навиты в одну сторону две нити, пропущенные через блоки M и N и несущие на концах два одинаковых груза m1и m2. Эти грузы действуют, как пара сил, приложенных в точках одного и того же диаметра диска.
С диском жестко связано зеркальце, поворачивающееся на некоторый угол при закручивании проволоки под влиянием приложенной пары сил. Поворот зеркальца фиксируется на шкале S, по которой перемещается отраженный от зеркальца световой “зайчик”.
Если при равновесии нить совпадает с делением no, а после поворота с делением n, то при малых углах поворота имеет место соотношение:
φo = (n—no)/2d (6)
Здесь d — расстояние от зеркальца до шкалы, выраженное в тех же единицах длины, что и деления на шкале.
Подставляя значение момента M = 2PR и G из (5) в равенство (1) и решая его относительно G, будем иметь
G = 4rPIo/π ro4 φo (7)
Угол закручивания определяется по формуле (6). Другие, входящие в формулу (7) величины, измеряются непосредственно.
Измерения
При помощи отвеса установить стойку прибора в вертикальном направлении. Установить трубу осветителя так, чтобы видеть на шкале отражение “зайчика” от зеркальца. При этом шкала должна быть перпендикулярна к оси трубы.
Малым поворотом трубы осветителя добиваются того, чтобы один край светового зайчика был наиболее резким, по этому краю и следует делать отсчет. Записывают нулевой отсчет no т. е. деление шкалы, на которое приходится резкий край “зайчика” до подвешивания грузов. Прикрепив к концам нитей платформы, нагружают их грузами, записывают отсчет по шкале n, соответствующий новому положению равновесия (веса грузов на платформе должны быть между собой примерно равны), и затем, сняв грузы, вновь производят нулевой отсчет no. Подобные измерения повторяют для двух, трех и т. д. грузов, каждый раз предварительно определяя нулевой отсчет.
Проделав измерение с максимальным грузом, повторяют измерения в обратном порядке, постепенно уменьшая величину грузов на платформах. За угол закручивания, соответствующий тому или иному грузу, берут среднее значение из измерений в одном и другом направлениях.
(штрихами отмечены отчеты, производящиеся при уменьшении грузов). Измеряют расстояние d от зеркальца до шкалы, определяют вес платформ и грузов, вычисляют модуль кручения для каждой нагрузки. Сравнивая значения модуля кручения, полученные при различных моментах сил, убеждаются, что все они имеют приблизительно одинаковое значение, т. е. в пределах применявшихся нагрузок, закон Гука выполняется.
После этого, промерив все входящие в формулу (7) величины, вычисляют модуль сдвига. Измерения диаметра стержня следует произвести в нескольких местах.
Контрольные вопросы
1. Что такое модуль сдвига, модуль кручения?
2. В работе описана методика измерения модуля кручения, какие из полученных значений можно считать наиболее точными?
Библиографический список
Физический практикум. Механика и молекулярная физика. 1967 г.
Стрелков курс физики. Том 1. Механика. 1956.
Определение модуля сдвига при испытании на кручение
Цель работы. Экспериментальное определение модуля сдвига стали и алюминиевого сплава Д16-Т.
1. Краткие теоретические сведения.
Расчеты на сдвиг (срез) выполняются для таких элементов конструкций, как сварные швы, заклепки, болты и др. При деформации сдвига возникают касательные напряжения τ, которые по закону Гука пропорциональны углу сдвига γ:
 ,
,
где  – модуль сдвига (модуль упругости второго рода).
– модуль сдвига (модуль упругости второго рода).
Модуль сдвига  связан с модулем продольной упругости (модулем упругости первого рода) соотношением:
связан с модулем продольной упругости (модулем упругости первого рода) соотношением:

где  – коэффициент поперечной деформации (коэффициент
– коэффициент поперечной деформации (коэффициент
Пуассона), для сталей  =0,25 … 0,30.
=0,25 … 0,30.
Частным случаем чистого сдвига являются деформации кручения валов и стержней круглого поперечного сечения. Однако в случае кручения удобнее фиксировать не угол сдвига материала, а угол закручивания стержня φ. Закон Гука при кручении стержней круглого поперечного сечения выражается формулой  ,
,
где  — угол закручивания или угол поворота одного сечения
— угол закручивания или угол поворота одного сечения
стержня относительно другого (рад),
 — расстояние между этими сечениями,
— расстояние между этими сечениями,
 — крутящий момент, передаваемый на стержень,
— крутящий момент, передаваемый на стержень,
 — полярный момент инерции поперечного сечения стержня.
— полярный момент инерции поперечного сечения стержня.
Зная величину  и вычислив полярный момент инерции сечения стержня
и вычислив полярный момент инерции сечения стержня  , можно по замеренному углу закручивания
, можно по замеренному углу закручивания  , соответствующему заданной моментной нагрузке, вычислить значение величины
, соответствующему заданной моментной нагрузке, вычислить значение величины  по формуле
по формуле

2. Применяемая установка и приборы
Для проведения работы используется наладка универсального лабораторного стенда по сопротивлению материалов СМ-2 (рис. 1).
Исследуемый образец 1 в виде ступенчатого трубчатого стержня, узкая часть которого выполнена из стали, а широкая из алюминиевого сплава Д16-Т (рис. 2), жестко соединяется со стойкой, выполненной в виде опоры типа «заделка». Противоположный конец образца имеет шарнирную опору, которая создается шарикоподшипником, опирающимся на другую стойку (на схеме не показаны). Нагружение осуществляется грузами, подвешиваемыми к концу рычага 2. Рычаг служит для нагружения образца крутящим моментом, величина которого:

где  – вес грузов, Н;
– вес грузов, Н;  – длина рычага, м.
– длина рычага, м.
Измерение угла закручивания  одного сечения относительно другого производится на рабочей части образца длиной
одного сечения относительно другого производится на рабочей части образца длиной  , где при помощи неподвижных захватов закреплен измеритель. Один из захватов имеет неподвижный кронштейн 6, на котором установлен индикатор часового типа 4. Другой захват имеет жесткую скобу 3, в которую упирается ножка индикатора 4.
, где при помощи неподвижных захватов закреплен измеритель. Один из захватов имеет неподвижный кронштейн 6, на котором установлен индикатор часового типа 4. Другой захват имеет жесткую скобу 3, в которую упирается ножка индикатора 4.
При повороте сечения В относительно сечения С индикатор фиксирует изменение величины  . Зная
. Зная иН, можно вычислить искомый угол закручивания образца между этими сечениями:
иН, можно вычислить искомый угол закручивания образца между этими сечениями:

Основные размеры установки:
Длина рычага a = 100 мм; длина образца L = 240 мм;
длина рабочей части образца l = 100 мм;
расстояние от оси образца до ножки индикатора H = 80 мм, наружный диаметр трубы из сплава Д16-Т D = 42 мм;
внутренний диаметр трубы из сплава Д16-Т D1= 40 мм;
наружный диаметр стальной трубы d = 20 мм,
внутренний диаметр стальной трубы d1 = 16 мм.

Рис. 1. Схема экспериментальной установки:
1 — ступенчатый стержень трубчатого сечения (участок ВС выполнен из стали, ДК – из алюминиевого сплава Д16-Т) , 2-грузовой рычаг, 3— скоба, 4— индикатор часового типа, 5— розетка тензорезисторов, 6 – кронштейн.
стальная труба Вид К



Рис. 2. Сечениястержня Рис. 3. Схема наклейки тензорезисторов
Рассмотрим элемент на поверхности бруса, который находится в напряженном состоянии «чистый сдвиг». Расчетное касательное напряжение 

 (где
(где — крутящий момент, передаваемый на образец,
— крутящий момент, передаваемый на образец, — полярный момент сопротивления кручению).
— полярный момент сопротивления кручению).
Для определения модуля сдвига участка стержня сплава Д16-Т в выбранной точке на поверхности образца (вид по стрелке К) наклеиваются три проволочных датчика сопротивления, составляющих розетку по схеме, приведенной на рис. 3.
Поскольку при кручении в сечениях, перпендикулярных оси стержня возникают касательные напряжения τ, а по сечениям, наклоненным к оси на угол 45º, действуют главные напряжения  и
и  , то деформации в направлении осей u и v на рис. 3
, то деформации в направлении осей u и v на рис. 3  и
и  будут главными. Используя тензометрический метод, главные напряжения на поверхности трубы из сплава Д16-Т найдем через главные деформации.
будут главными. Используя тензометрический метод, главные напряжения на поверхности трубы из сплава Д16-Т найдем через главные деформации.
Определим продольную деформацию в диагональном направлении (под углом 45 0 к оси бруса), как отношение удлинения диагонали
∆ℓ =  к ее первоначальной длине ℓ =
к ее первоначальной длине ℓ = (рис. 4). В результате получим:
(рис. 4). В результате получим:

В направлении другой диагонали деформация будет отличаться только знаком, т.е.  или
или .
.

Рис. 4. Схема деформации стержня в точке наклейки
В результате модуль сдвига сплава Д16-Т может быть определен по формуле: 
где  и
и – продольные деформации, определяемые электротензометрическим методом.
– продольные деформации, определяемые электротензометрическим методом.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
ПРИ КРУЧЕНИИ



Отчет по лабораторной работе
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА
ПРИ КРУЧЕНИИ
Выполнили ст. гр. АГПС-11:
Проверил: Шабей М.М.
.Цель работы:
Экспериментальная проверка закона Гука при сдвиге и определение модуля сдвига материала вала.
Содержание работы:
Рассмотрим схему вала, работающего на кручение. На одном конце вал защемлен, на другом нагружен сосредоточенным крутящим моментом (рис.1).
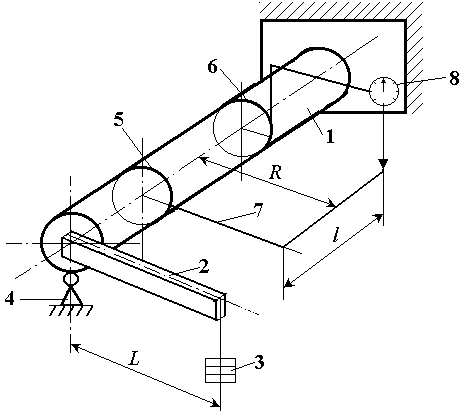 |
Рис. 1. Схема вала, нагруженного крутящим моментом.
Угол поворота сечения 5 относительно сечения 6 на участке вала постоянного поперечного сечения с крутящим моментом Мкр определяется формулой
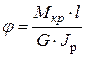 (1)
(1)
Здесь l– расстояние между сечениями вала, G– модуль сдвига. Полярный момент инерции Jp определяется по формуле:
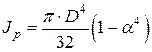 (2)
(2)
где α= d/ D — отношение внутреннего d и наружного D диаметров сечений.
Крутящий момент создается подвешиванием грузов 3 весом Р к рычагу 2 с плечом L
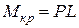 (3)
(3)
Угол поворота φ сечения 5 относительно сечения 6 рассчитывается по перемещению Δ, измеряемому индикатором часового типа 8:
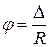 (4)
(4)
Линейная зависимость (1) между углом поворота и крутящим моментом сохраняется, пока напряжения в материале вала не превосходят предела текучести. Касательные напряжения на наружной поверхности вала при данном крутящем моменте подсчитываются по формуле:
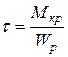 (5)
(5)
где Wp— полярный момент сопротивления, 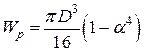
Угловые деформации на наружной поверхности вала можно определить через угол поворота φ:
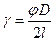 (6)
(6)
Теоретическое значение модуля сдвига может быть вычислено по значениям модуля Юнга и коэффициента Пуассона:
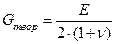 (7)
(7)
Оборудование и материалы:
1. Установка ТМт 11/14 для определения модуля сдвига при кручении и главных напряжений при кручении и совместном действии изгиба и кручения.
2. Индикатор часового типа ИЧ–10.
3. Грузы подвесные.
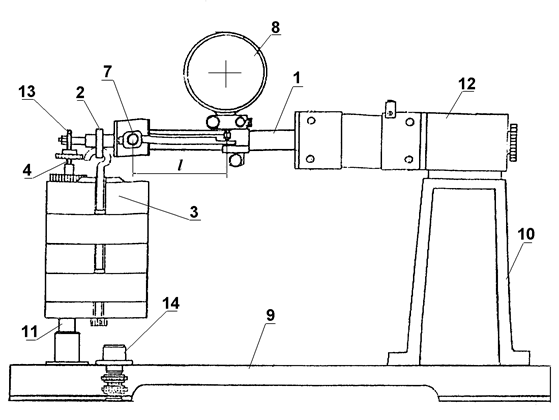 |
Установка ТМт 11/14 (см. рис. 2) выполнена в настольном исполнении и состоит из сварного основания 9, на котором справа закреплена стойка 10 в виде усеченной пирамиды, а слева закреплена цилиндрическая стойка 11 с винтом 4. На стойке 10 установлен корпус 12 с полым ступенчатым валом 1, свободный конец которого шарикоподшипником 13 опирается на регулировочный винт 4 левой стойки. На рабочем участке вала 1 установлена индикаторная головка 8 часового типа для измерения угловых перемещений вала после нагружения его подвесом 3 с гирями через рычаг 2. Для устойчивости установки имеется поворотная опора 14. закрепленная на основании 9. Для исследования напряженного состояния в стержне при кручении и при совместном действии изгиба и кручения используют трубу из алюминиевого сплава Д16Т с наружным диаметром 46 мм и внутренним – 44 мм.
Рис. 2. Установка ТМт 11/14.
Для определения модуля сдвига исследуется образец кольцевого поперечного сечения с длиной рабочего участка l (мм).
Материал образца – сталь 45 с модулем упругости Е= 2·10 5 МПа
и коэффициентом Пуассона ν = 0,3.
Внутренний диаметр d=14 мм;
наружный диаметр D=20 мм;
радиус вылета рычага угломера (расстояние от оси вала до головки индикатора часового типа) R =100 мм.
Цена одного деления индикатора часового типа – 0,01 мм. Один оборот большой стрелки соответствует вертикальному перемещению штока индикатора на 1 мм. Полный рабочий ход штока – 10 мм.
Меры безопасности:
К работе с указанной установкой допускаются лица, ознакомленные с её устройством, принципом действия и порядком проведения работы.
Задание для выполнения:
Произвести замеры показаний индикатора часового типа при следующих значениях массы груза 3 (рис. 2): 1, 2, 3, 4, 5 кг.