Модуль упругости алюминия КГ см2
Расчетные сопротивления и модули упругости для различных строительных материалов
При расчете строительных конструкций нужно знать расчетное сопротивление и модуль упругости для того или иного материала. Здесь представлены данные по основным строительным материалам.
Таблица 1. Модули упругости для основных строительных материалов.
| Материал | Модуль упругости Е, МПа |
| Чугун белый, серый | (1,15. 1,60) • 10 5 |
| » ковкий | 1,55 • 10 5 |
| Сталь углеродистая | (2,0. 2,1) • 10 5 |
| » легированная | (2,1. 2,2) • 10 5 |
| Медь прокатная | 1,1 • 10 5 |
| » холоднотянутая | 1,3 • 10 3 |
| » литая | 0,84 • 10 5 |
| Бронза фосфористая катанная | 1,15 • 10 5 |
| Бронза марганцевая катанная | 1,1 • 10 5 |
| Бронза алюминиевая литая | 1,05 • 10 5 |
| Латунь холоднотянутая | (0,91. 0,99) • 10 5 |
| Латунь корабельная катанная | 1,0 • 10 5 |
| Алюминий катанный | 0,69 • 10 5 |
| Проволока алюминиевая тянутая | 0,7 • 10 5 |
| Дюралюминий катанный | 0,71 • 10 5 |
| Цинк катанный | 0,84 • 10 5 |
| Свинец | 0,17 • 10 5 |
| Лед | 0,1 • 10 5 |
| Стекло | 0,56 • 10 5 |
| Гранит | 0,49 • 10 5 |
| Известь | 0,42 • 10 5 |
| Мрамор | 0,56 • 10 5 |
| Песчаник | 0,18 • 10 5 |
| Каменная кладка из гранита | (0,09. 0,1) • 10 5 |
| » из кирпича | (0,027. 0,030) • 10 5 |
| Бетон (см. таблицу 2) | |
| Древесина вдоль волокон | (0,1. 0,12) • 10 5 |
| » поперек волокон | (0,005. 0,01) • 10 5 |
| Каучук | 0,00008 • 10 5 |
| Текстолит | (0,06. 0,1) • 10 5 |
| Гетинакс | (0,1. 0,17) • 10 5 |
| Бакелит | (2. 3) • 10 3 |
| Целлулоид | (14,3. 27,5) • 10 2 |
Примечание: 1. Для определения модуля упругости в кгс/см 2 табличное значение умножается на 10 (более точно на 10.1937)
2. Значения модулей упругости Е для металлов, древесины, каменной кладки следует уточнять по соответствующим СНиПам.
Нормативные данные для расчетов железобетонных конструкций:
Таблица 2. Начальные модули упругости бетона (согласно СП 52-101-2003)

Таблица 2.1. Начальные модули упругости бетона согласно СНиП 2.03.01-84*(1996)
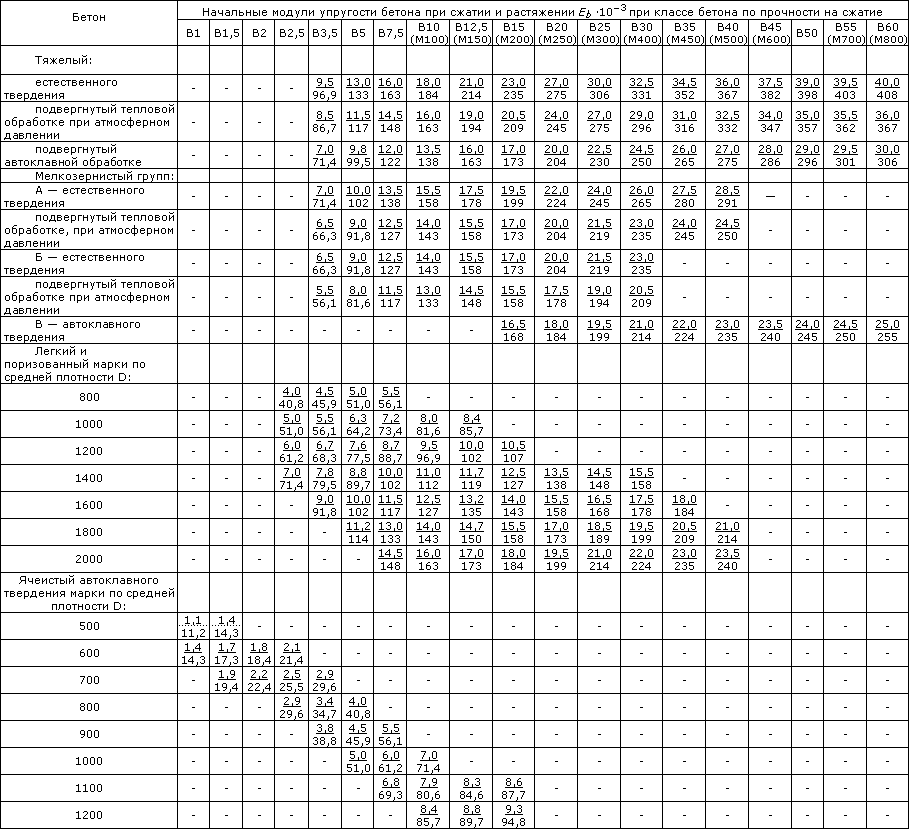
Примечания: 1. Над чертой указаны значения в МПа, под чертой — в кгс/см 2 .
2. Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции.
3. Для ячеистого бетона неавтоклавного твердения значения Еb принимают как для бетона автоклавного твердения с умножением на коэффициент 0,8.
4. Для напрягающего бетона значения Еb принимают как для тяжелого бетона с умножением на коэффициент a = 0,56 + 0,006В.
5. Приведенные в скобках марки бетона не точно соответствуют указанным классам бетона.
Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003)

Таблица 4. Расчетные значения сопротивления бетона (согласно СП 52-101-2003)

Таблица 4.1. Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)
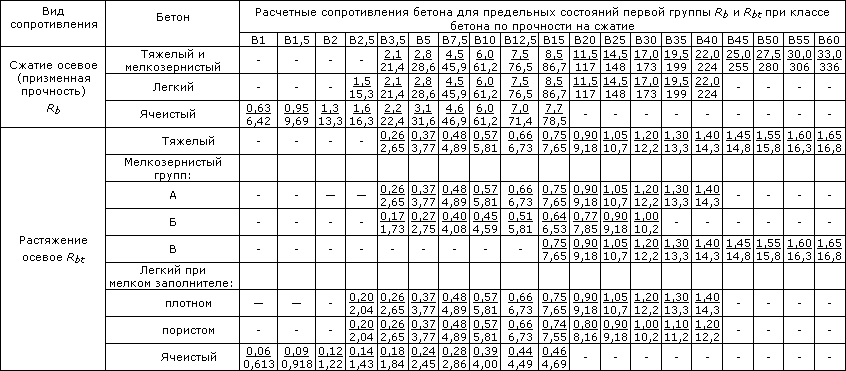
Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)

Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)

Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)

Таблица 6.2. Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
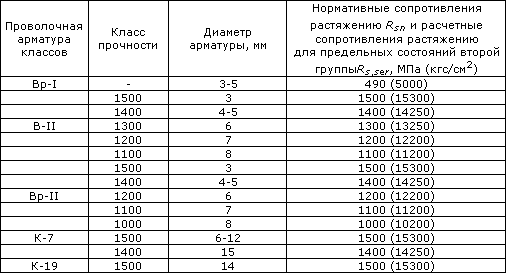
Таблица 7. Расчетные сопротивления для арматуры(согласно СП 52-101-2003)
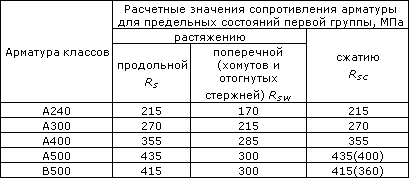
Таблица 7.1. Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
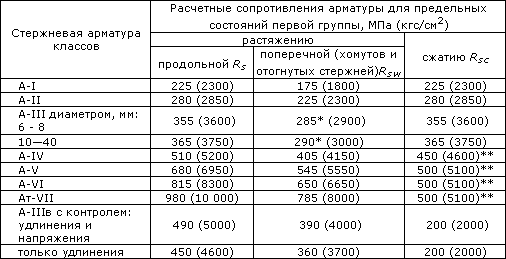
Таблица 7.2. Расчетные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
Нормативные данные для расчетов металлических конструкций:
Таблица 8. Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе (согласно СНиП II-23-81 (1990))
листового, широкополосного универсального и фасонного проката по ГОСТ 27772-88 для стальных конструкций зданий и сооружений
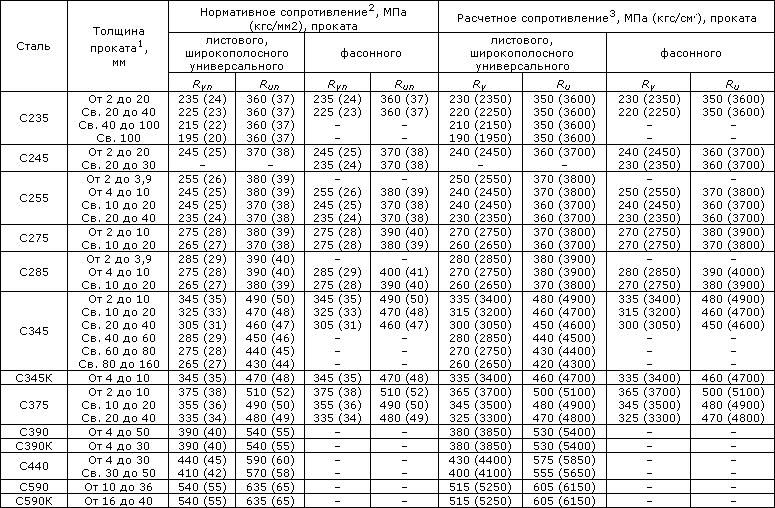
Примечания:
1. За толщину фасонного проката следует принимать толщину полки (минимальная его толщина 4 мм).
2. За нормативное сопротивление приняты нормативные значения предела текучести и временного сопротивления по ГОСТ 27772-88.
3. Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициенты надежности по материалу, с округлением до 5 МПа (50 кгс/см 2 ).
Таблица 9. Марки стали, заменяемые сталями по ГОСТ 27772-88 (согласно СНиП II-23-81 (1990))
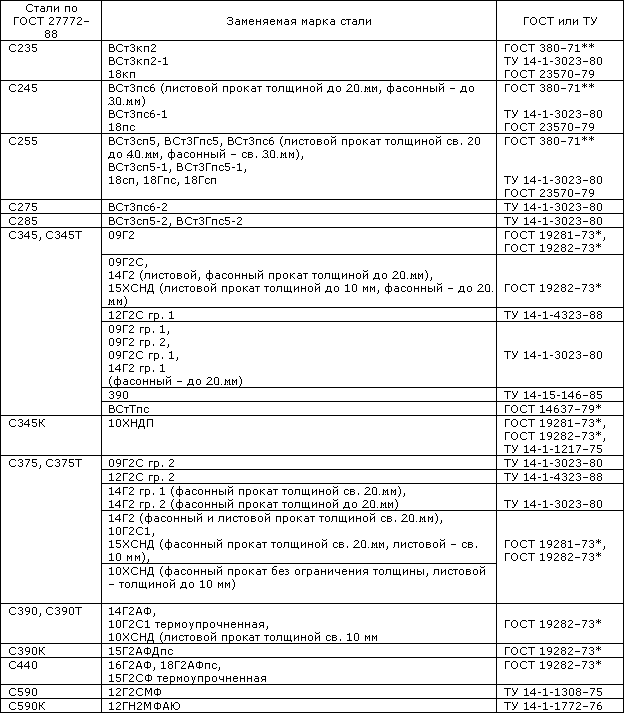
Примечания: 1. Стали С345 и С375 категорий 1, 2, 3, 4 по ГОСТ 27772-88 заменяют стали категорий соответственно 6, 7 и 9, 12, 13 и 15 по ГОСТ 19281-73* и ГОСТ 19282-73*.
2. Стали С345К, С390, С390К, С440, С590, С590К по ГОСТ 27772-88 заменяют соответствующие марки стали категорий 1-15 по ГОСТ 19281-73* и ГОСТ 19282-73*, указанные в настоящей таблице.
3. Замена сталей по ГОСТ 27772-88 сталями, поставляемыми по другим государственным общесоюзным стандартам и техническим условиям, не предусмотрена.
Расчетные сопротивления для стали, используемой для производства профилированных листов, приводятся отдельно.
1. СНиП 2.03.01-84 «Бетонные и железобетонные конструкции»
3. СНиП II-23-81 (1990) «Стальные конструкции»
4. Александров А.В. Сопротивление материалов. Москва: Высшая школа. — 2003.
5. Фесик С.П. Справочник по сопротивлению материалов. Киев: Будiвельник. — 1982.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630
спасибо вам всеесть то что надо
Почему значения начального модуля упругости бетона при сжатии и растяжении умножаются на 10^-3? Должна ведь быть положительная степень. Выходит, что модуль упругости для бетона В25 составляет 30 кПа, но он равен 30 ГПа!
Потому, что при составлении разного рода таблиц нет необходимости писать в каждой ячейке по 3 дополнительных нуля, достаточно просто указать, что табличные значения занижены в 1000 раз. Соответственно, чтобы определить расчетное значение, нужно табличное значение не разделить, а умножить на 1000. Такая практика используется при составлении многих нормативных документов (именно в таком виде там даются таблицы) и я не вижу смысла от нее отказываться.
Тогда получается, что модуль упругости арматуры необходимо разделить на 10 в пятой степени. Или я что-то не понимаю? В рекомендациях по расчету и конструированию сплошных плит перекрытий крупнопанельных зданий 1989г. и модуль бетона и модуль арматуры умножают на 10 в третьей и на 10 в пятой степени соответственно
Попробую объяснить еще раз. Посмотрите внимательно на таблицу 1. Если бы в заглавной строке вместо «Модуль упругости Е, МПа» я бы прописал «Модуль упругости Е, МПа•10^-5», то это избавило бы меня от необходимости в каждой строке к значению модуля упругости добавлять «•10^5». Вот только значения модулей упругости для различных материалов различаются в сотни и даже тысячи раз, потому такая форма записи для таблицы 1 не совсем удобна. В таблицах 2 и 2.1 значения начальных модулей упругости различаются незначительно и потому использовалась такая форма записи. Более того, если вы откроете указанные нормативные документы, то лично в этом убедитесь. Традиция эта сформировалась в ту далекую пору, когда ПК и в помине не было и наборщик вручную набирал литеры в пресс для книгопечатания, так что в данном случае все вопросы не ко мне, а к Гутенбергу и его последователям.
Возможно, модуль упругости легче бы запоминался и воспринимался в ГПа, ведь тогда у стали примерно 200 единиц, а у древесины 10. 12.
Вполне возможно, вот только и ГигаПаскали — не самая наглядная и простая для восприятия размерность.
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Статьи
Свойства алюминия
Свойства алюминия
Алюминий — серебристо-белый легкий металл. Расположен в III группе Периодической системы элементов Д.И.Менделеева под номером 13; атомная масса алюминия — 26,98. Конфигурация внешней электронной оболочки 3s 2 3р; атомный радиус — 0,143 мм, ионный радиус А1 3+ (в скобках указаны координационные числа) 0,053 нм (4); 0,062 нм (5); 0,067 нм (6); энергия ионизации А1 -» А1 + -> А1 2+ —> А1 3+ — соответственно 5,984; 18,828; 28,44 эВ; сродство к электрону 0,5 эВ; электроотрицательность по Поллингу — 1,5; поперечное сечение захвата тепловых нейтронов — 215*10 -25 м 2 [3]. Алюминий имеет кубическую гранецентрированную кристаллическую решетку с параметрами: а = 0,40403 нм, z = 4, пространственная группа Fm3m. В природе существует один стабильный изотоп 27 А1.
Отличительные особенности алюминия — высокая электропроводимость, теплопроводность, коррозионная стойкость, малая плотность и отличная обрабатываемость давлением в холодном состоянии.
Физические свойства алюминия [2-6]
Механические свойства алюминия [4-6]
При охлаждении алюминия до температуры ниже 120 К его прочностные свойства в отличии от большинства металлов возрастают, а пластичность не изменяется (табл. 1.7).
Механические свойства алюминия различной чистоты
| Состояние | Содержание Аl, % | Предел прочности при растяжении σв2МПа | Предел текучести при растяжении σ.00,2, МПа | Относительное удлинение δ, % | Твердость по Бринеллю, НВ |
| Литой в землю | 99,996 | 50 | — | 45 | 13-15 |
| Литой в землю | 99,5 | 75 | — | 29 | 20 |
| Литой в землю | 99.0 | 85 | — | 20 | 25 |
| Литой в кокиль | 99,0 | 90 | — | 25 | 25 |
| Деформированный и отожженный | 99.0 | 90 | 30 | 30 | 25 |
| Деформированный | 99,0 | 140 | 100 | 12 | 32 |
| Литой в землю | 98,0 | 90 | 35 | 12,5 | 28 |
Технологические свойства алюминия [6]
Коррозионные свойства алюминия [6].
Алюминий и его сплавы характеризуются высокой коррозионной стойкостью в атмосферных условиях как сельской местности, так и городских промышленных районов.
Сернистый газ, сероводород, аммиак и другие газы, находящиеся в воздухе промышленных районов, не оказывают заметного влияния на скорость коррозии алюминия и его сплавов. Алюминий практически не корродирует в дистиллированной и чистой пресной (естественной) воде даже при высоких температурах (до 180 °С). Действие пара на алюминий и его сплавы также незначительно.
Вода, содержащая примеси щелочей, резко повышает скорость коррозии алюминия. При комнатной температуре скорость коррозии алюминия в аэрированной воде содержащей 0,1% едкого натрия — 16 мм/год; 0,1% соляной кислоты — 1 мм/год и 1% соды — 4 мм/год.
Алюминий и его сплавы, не содержащие меди, достаточно стойки в естественной (не загрязненной) морской воде. Сернокислые соли магния, натрия, алюминия, а также гипосульфит практически не действуют на технический алюминий. Скорость коррозии алюминия возрастает в присутствии в воде солей ртути, меди или ионов хлора, разрушающих защитную оксидную пленку на алюминии.
В концентрированной азотной кислоте при комнатной температуре алюминий и его сплавы устойчивы, но быстро разрушаются в разбавленных кислотах.
Слабые растворы серной кислоты, концентрацией до 10%, при комнатной температуре незначительно влияют на технический алюминий, но с повышением концентрации и температуры скорость коррозии резко возрастает. В концентрированной серной кислоте алюминий практически устойчив.
Соляная кислота быстро разрушает алюминий и его сплавы, особенно с повышением температуры. Такое же действие на алюминий оказывают растворы плавиковой и бромистоводородной кислот. Слабые растворы фосфорной (менее 1%), хромовой (до 10%) и борной (при всех концентрациях) кислот на алюминий и его сплавы действуют незначительно.
Органические кислоты — уксусная, масляная, лимонная, винная, а также кислые (незагрязненные) фруктовые соки, вино оказывают слабое действие на алюминий и его сплавы, за исключением щавелевой и муравьиной кислот.
Алюминий и его сплавы быстро разрушаются в растворах едких щелочей, однако в растворах аммиака они довольно стойки, особенно сплавы, содержащие магний. Амины на них действуют также незначительно.
Следует отметить, что алюминий и однофазные сплавы на алюминиевой основе более стойки в коррозионном отношении, чем сплавы двухфазные и многофазные.
Влияние примесей на свойства алюминия. На коррозионные, физические, механические и технологические свойства алюминия оказывают значительное влияние примеси различных элементов. Так, например, большинство примесей снижают электропроводность алюминия (рис. 1.1). Основные примеси в алюминии — железо и кремний. Железо снижает коррозионную стойкость, электропроводность и пластичность алюминия, но несколько повышает его прочность. Диаграмма состояния системы Al-Fe, приведенная на рис. 1.2, показывает, что железо незначительно растворяется в алюминии в твердом состоянии. При температуре эвтектики (655°С) растворимость железа достигает 0,052% и с понижением температуры граница твердого раствора а резко сдвигается в сторону алюминия. Железо в алюминии присутствует в виде самостоятельной фазы Al3Fe.
Железо — вредная примесь не только в алюминии, но и в сплавах алюминия с кремнием и магнием. Однако в жаропрочных алюминиевых сплавах железо (в сочетании с никелм) является полезной примесью.
Обычная примесь в алюминии — кремний. В сплавах на алюминиевой основе кремний наряду с медью, магнием, цинком, а также марганцем, никелем и хромом вводится в качестве основного компонента. Образующиеся при этом соединения CuAl2, Mg2Si, CuMgAl2 и др. являются эффективными упрочнителями алюминиевых сплавов.
Из диаграммы состояния алюминий-кремний (рис. 1.3) видно, что при температуре эвтектики 577°С в алюминии растворяется до 1,65% кремния. С понижением температуры область твердого раствора α резко уменьшается.

Примеси кальция и других элементов, присутствующих в стандартных марках алюминия в незначительном количестве, не имеют практического значения. Небольшие добавки церия, натрия и титана оказывают существенное влияние на структуру и свойства определенных алюминиевых сплавов.
Водород хорошо растворяется в алюминии и оказывает отрицательное влияние на его свойства, вызывая при литье пористость. Азот при высоких температурах вступает в реакцию с алюминием с образованием тугоплавкого соединения.
Токсикологические свойства алюминия [7]. В соответствии с ГОСТом по степени воздействия на организм человека алюминиевую пыль относят к III классу опасности. Предельно-допустимая концентрация (ПДК) в воздухе пыли металлического алюминия и его оксидов составляет 2 мг/м 3 .
При постоянном вдыхании пыли металлического алюминия и его оксида может возникнуть алюминоз легких. Рабочие, подвергшиеся воздействию пыли, должны проходить периодически флюорографическое обследование. У рабочих, занятых в производстве алюминия, часты катары верхних дыхательных путей (рипиты, фарингиты).
Наибольшую опасность для здоровья представляет процесс электролиза глинозема, протекающий в расплавленном криолите (Na3AlF6) при температуре 950 °С. Электролиз расплавленных солей может сопровождаться выбросами большого количества фторидной пыли, фторсодержащих газов, а также паров и частиц битума-компонента анодной массы. Рабочим, занятым на этой операции, также грозят ожоги кожи и глаз при попадании на них расплавленного металла. Во избежании несчастных случаев электролизные ванны необходимо надежно изолировать, рабочие должны иметь средства индивидуальной защиты:, противопылевые маски, очки. перчатки, фартуки, сапоги и т.д. В электролизных цехах должен регулярно проводиться контроль за содержанием пыли в воздухе.
ПДК алюминия и его оксида по ГОСТу и нормативам США приведены ниже:
* Предел кратковременного влияния, т.е. максимальная концентрация, воздействию которой человек может подвергаться не более 15 минут подряд при условии, что в течении дня допускается не более 4-х таких воздействий с промежутками не менее 60 минут.
** Величина порогового предела концентрации вещества, устанавливаемая американской конференцией государственных гигиенистов и определенная для 8-часового рабочего дня и 40-часовой рабочей недели.
Модуль Юнга
Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела.
Это свойство любого материала, и оно зависит от температуры и оказываемого давления.
В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации.
Другими словами: когда тело деформируется, то появляется сила, которая стремится восстановить первоначальную форму и размер тела. Сила упругости является этой проявляющейся силой. Также она представляет собой следствие электромагнитного взаимодействия между частицами.
Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным.
Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.
Примеры значений модуля Юнга (упругости) для:
- (т.е. для резины он в 5 раз меньше стали)
Таблица
Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи «гигапаскалей» ([ГПа]; ).
| Материал | Модуль Юнга E, [ГПа] |
|---|---|
| Алмаз | 1220 |
| Алюминий | 69 |
| Дерево | 10 |
| Кадмий | 50 |
| Латунь | 97 |
| Медь | 110 |
| Никель | 207 |
| Резина | 0,9 (≈ 1 МПа, мегапаскаль) |
| Сталь | 200 |
| Титан | 107 |
Единица измерения и формулы
Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).
Формулы
Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.
Закон Гука
Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.
Закон Гука (этот описывает явления в теле, в дифференциальной форме):

- σ — механическое напряжение
- E — модуль Юнга (модуль упругости)
- ε — относительное удлинение
Закон Гука (этот описывает явления в теле)
- Fупр — сила упругости
- k × Δl — удлинение тела
- Fупр — сила упругости
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина тела
- Δl — удлинение тела
- Fупр/S — механическое напряжение, обозначается как σ
- Δl/l — относительное удлинение, обозначается как ε
Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму. В какой точке это происходит, уже зависит от материала. Если материал очень жёсткий (значит высокое показание модуля упругости), то эта точка может совпадать с разрывом/деформацией.
Другие формулы вычисления модуля Юнга (модуля упругости)
- E — модуль Юнга (модуль упругости)
- k — жёсткость тела
- l — первоначальная длина стержня
- S — площадь поперечного сечения
Либо можно выразить k (жёсткость тела):
- k — жёсткость тела
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина стержня/тела
Пример решения задачи (через закон Гука):
Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.
- l = 2,5 м
- F = 50 H
- E = ?
Будем искать через закон Гука (σ = E × ε).
Помним из закона Гука:
σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)
ε = Δl/l (а это относительное удлинение, обозначается как ε)
Подставляем в формулу (σ = E × ε):
Например, в нашей таблице такой модуль Юнга имеет кадмий.
Способы определения и контроля показателей прочности металлов
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
- Виды нагрузок
- Понятие о модуле упругости
- Таблица 1: Модуль упругости для металлов и сплавов
- Модуль упругости для разных марок стали
- Таблица 2: Упругость сталей
- Модули прочности
- Таблица 3: Модули прочности для сталей
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
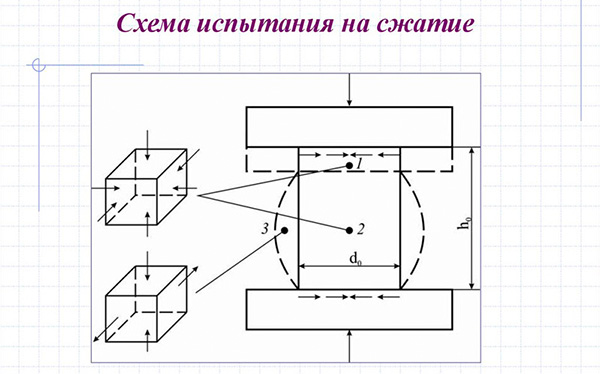
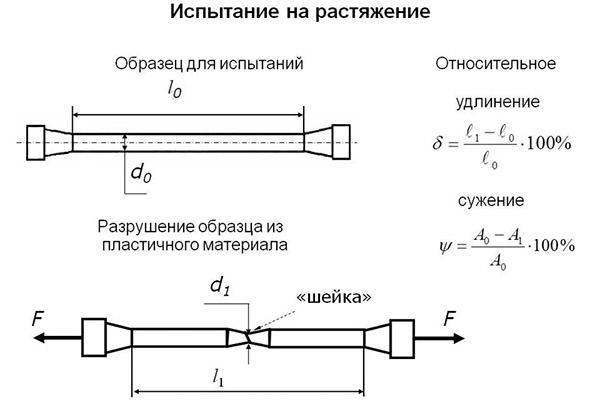
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
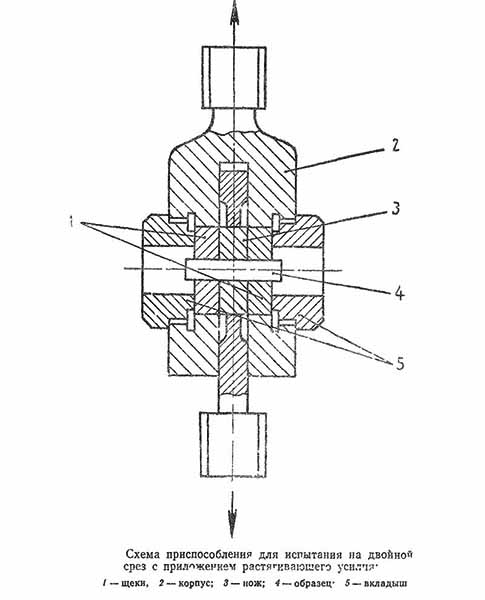
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
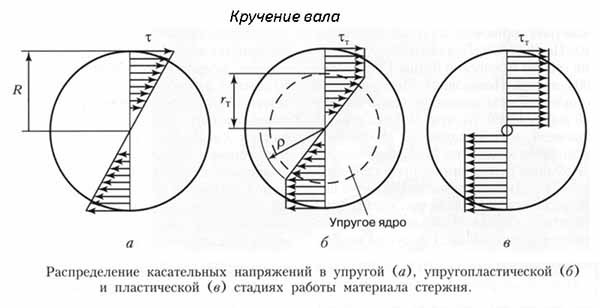
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.

Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
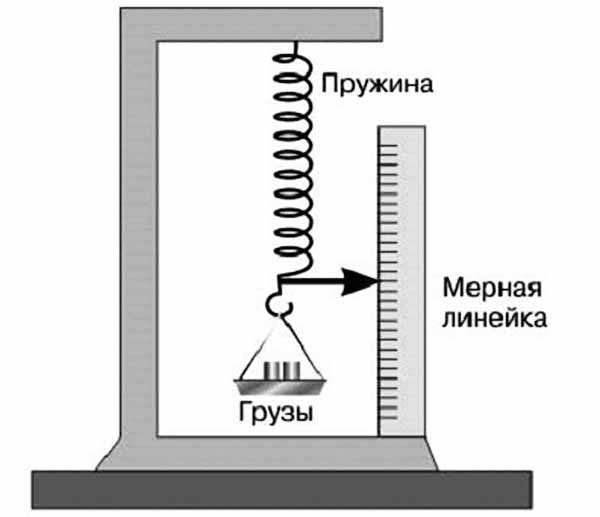
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Модуль упругости разных материалов, включая сталь
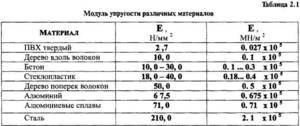 Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости — что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
 Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.- Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
- Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
- Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
 Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.
Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.
После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.
Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:
- Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см^2.
- Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см^2.
- Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см^2. Для холодно-сплющенной арматуры показатели аналогичны.
- Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см^2
- Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см^2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см^2 .
- Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см^2 .
- И напоследок коэффициент Пуассона для стали равен значению 0,3
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Сталь и несколько разных её марок
| Материал | Показатели модуля упругости (Е, G; Н*м2, кг/см^2, МПа) |
| Сталь | 20,6*10^10 ньютон*метр^2 |
| Сталь углеродистая | Е=(2,0…2,1)*10^5 МПа; G=(8,0…8,1)*10^4 МПа |
| Сталь 45 | Е=2,0*10^5 МПа; G=0,8*10^5 МПа |
| Сталь 3 | Е=2,1*10^5 МПа; G=0,8*10^5 МПа |
| Сталь легированная | Е=(2,1…2,2)*10^5 МПа; G=(8,0…8,1)*10^4 МПа |
 Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.
Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.
Кстати, если не выражать все значения числовыми отношениями, а взять сразу и посчитать полностью, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.
Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.
Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.
Модуль упругости
Из Википедии — свободной энциклопедии
Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:
E = def d σ d ε
- E — модуль упругости;
- σ
— напряжение, вызываемое в образце действующей силой (равно силе, делённой на площадь приложения силы);
- ε
— упругая деформация образца, вызванная напряжением (равна отношению изменения размера образца после деформации к его первоначальному размеру).
В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука):
E = σ ε 
Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:
- Модуль Юнга ( E ) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия (удлинения). Часто модуль Юнга называют просто модулем упругости.
- Модуль сдвига или модуль жесткости ( G или μ
) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига является одной из составляющих явления вязкости.
- Модуль объёмной упругости или Модуль объёмного сжатия ( K ) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля (для несжимаемой жидкости — бесконечен).
Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.
В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.
или второй параметр Ламе
Модули упругости (Е) для некоторых веществ:

 Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
