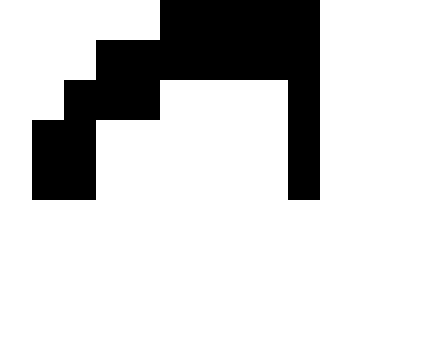Диаграмма напряжение деформация для стали

Диаграмма напряжение деформация для стали

Диаграммы нагружения и разгружения образцов. Закон повторного нагружения

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД иаграмма растяжения образца позволяет оценить поведение материала образца в упругой и упруго-пластической стадиях деформирования, определить механические характеристики материала.

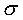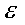&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД ля получения численно сопоставимых между собой механических характеристик материалов диаграммы растяжения образцов перестраивают в диаграммы растяжения материалов, т.е. в зависимость между напряжением &nbsp и деформацией &nbsp, которые определяют по формулам

&nbsp&nbsp&nbsp&nbsp&nbsp,

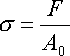
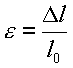где &nbsp- сила, действующая на образец,

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp- начальная площадь поперечного сечения и начальная длина расчетной части образца.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД иаграмма растяжения материала, полученная при этих условиях (без учета изменения размеров расчетной части образца), называется условной диаграммой растяжения материала в отличие от действительной диаграммы растяжения, которую получают с учетом изменений размеров образца.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД иаграмма растяжения материала зависит от его структуры, условий испытаний (температуры, скорости деформирования).

&nbsp&nbsp&nbsp

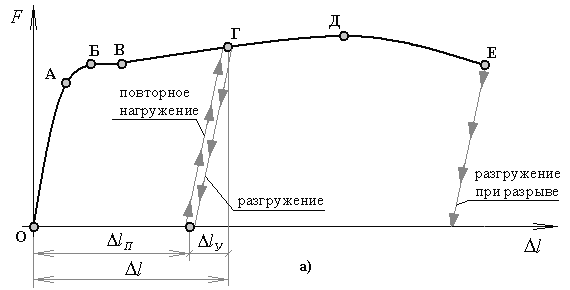
&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД иаграмма растяжения образца из низкоуглеродистой стали при однократном нагружении до разрушения. Конечная точка диаграммы соответствует разрушению.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspН а начальном участке диаграммы между силой &nbsp и удлинением 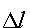&nbsp соблюдается прямая пропорциональная зависимость — образец подчиняется закону Гука. В точке А диаграммы закон Гука нарушается: зависимость между силой и удлинением становится нелинейной. На диаграмме наблюдается горизонтальный участок (участок БВ), называемый площадкой текучести. В этой стадии испытания образец удлиняется (деформируется) практически при постоянной силе. Это явление называется текучестью, при этом образец деформируется равномерно и по всей длине рабочей части. В точке В площадка текучести заканчивается и начинается участок упрочнения. В конечной точке Д этого участка достигается максимальная сила, которую может выдержать образец.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspП ри нагружении до предела пропорциональности (точка Г диаграммы) и при дальнешем уменьшении нагрузки образец разгружается по линейному закону, который совпадает с законом первичного нагружения. В этом заключается «закон разгрузки». При нагружении образца в пределах действия закона Гука законы нагружения и последующего разгружения совпадают. При полной разгрузке образца его размеры и форма возвращаются к первоначальной кривой однократного нагружения.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspН апряженное состояние образца до точки Д — одноосное.

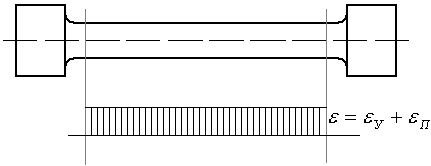
&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД алее начинается участок разрушения или участок местной текучести. Он характеризуется местным утонением образца и появлянием шейки.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspН а конечном участке ДЕ (после возникновения шейки) происходит локализация деформаций в шейке, в остальной части образца они практически не увеличиваются. Деформация в шейке неоднородная, имеет существенный градиент вдоль оси образца. Напряженное состояние на этом участке становится неоднородным, кроме того, оно изменяется качественно — становится трехосным. Диаметр шейки уменьшается по мере деформирования образца, и образец разрывается по наименьшему сечению шейки.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspЕ сли при испытании на растяжение нагружение приостановить, например, в точке Г диаграммы и осуществить разгружение образца, то окажется, что диаграмма разгружения и диаграмма предыдущего нагружения не совпадают. Линия разгружения в этом случае — прямая, параллельная начальному линейному участку диаграммы растяжения образца. Такой характер деформирования образца при его разгружении называется законом разгружения. При повторном нагружении диаграмма до точки Г совпадает с линией разгружения, а затем будет совпадать с диаграммой растяжения образца при однократном нагружении. Такой характер деформирования называется законом повторного нагружения и заключается в пропорциональной зависимости силы и удлинения, которая сохраняется до значения силы, достигнутой при первичном нагружении.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbsp П ри разгружении образца в пределах участка ОА законы нагружения, разгружения и повторного нагружения совпадают.

Диаграмма деформации при растяжении

Графическое изображение зависимости между напряжениями (или нагрузками) и деформациями материала (или перемещениями при деформировании) представляет собой диаграмму деформирования.

Испытательные машины имеют специальные приспособления, которые автоматически фиксируют диаграмму растяжения. На диаграмме по оси ординат откладываются действующие осевые нагрузки, а по оси абсцисс — абсолютные деформации.

На рис. 2.2 даны типичные диаграммы растяжения различных металлов. Диаграмма с постепенным переходом из упругой в пластическую область (рис. 2.2, а) свойственна большинству металлов в пластичном состоянии (легированные стали, медь, бронза).

Рис. 2.2. Диаграммы растяжения:

а — для большинства металлов в пластичном состоянии с постепенным переходом из упругой в пластическую область; б — для некоторых металлов в пластичном состоянии со скачкообразным переходом в пластическую область; в — для хрупких металлов

Пластичные материалы разрушаются при больших остаточных деформациях (больших остаточных удлинениях, измеряемых после разрыва).

Диаграмма со скачкообразным переходом в пластическую область в виде четко обозначенной «площадки» текучести (рис. 2.2, б) свойственна некоторым металлам. К таким металлам можно отнести мягкую углеродистую сталь, а также некоторые отожженные марганцовистые и алюминиевые бронзы.

Хрупкие материалы разрушаются при малых остаточных деформациях. К хрупким материалам можно отнести закаленную и неотпущенную сталь, серый чугун.

Характерные участки и точки диаграммы растяжения показаны на рис. 2.3. По оси абсцисс откладывают абсолютные удлинения А/ образца, а по оси ординат — значения растягивающей силы Р. Сначала получим на первом участке диаграммы 0—1 прямолинейную зависимость между силой и удлинением, что отражает закон Гука. При дальнейшем увеличении силы (за точкой 1) прямолинейная зависимость между Р и А/ нарушается. Точка 1 соответствует пределу пропорциональности, т. е. наибольшему напряжению, при котором еще соблюдается закон Гука. Если нагрузку, соответствующую точке 1, обозначить ,P_nu, а начальную площадь сечения образца Fq, то предел пропорциональности

Рис. 2.3. Характерные участки и точки диаграммы растяжения

Несколько выше точки 1 находится точка Г, соответствующая пределу упругости. Если нагрузку, соответствующую точке Г, обозначить через Р_уп, то предел упругости

По ГОСТу предел упругости задается и обозначается ag os — напряжение, при котором остаточное удлинение достигает 0,05 % длины участка образца, равного базе тензометра.

За точкой Г возникают уже заметные остаточные деформации. В точке 2 диаграммы частицы материала начинают переходить и область пластичности — наступает явление текучести образца.

На диаграмме растяжения получается горизонтальный участок 2—3 (площадка текучести), параллельный оси абсцисс. Для участка 2—3 характерен рост деформации без заметного увеличения нагрузки. Обозначим величину нагрузки, соответствующей площадке текучести 2—3, через Р_т. Напряжение а_т, отвечающее этой нагрузке, это то напряжение, при котором рост деформации происходит без заметного увеличения нагрузки, оно и является физическим пределом текучести.

Предел текучести (физический) — это механическая характеристика материалов: напряжение, отвечающее нижнему положению площадки текучести в диаграмме растяжения для материалов, имеющих эту площадку (см. рис. 2.3):

Предел текучести устанавливает границу между упругой и упруго-пластической зонами деформирования.

Даже небольшое увеличение напряжения (нагрузки) выше предела текучести вызывает значительные деформации.

Для материалов, не имеющих на диаграмме площадки текучести, принимают условный предел текучести: напряжение, при котором остаточная деформация образца достигает определенного значения, установленного техническими условиями (большего, чем это установлено для предела упругости).

Обычно допуском для величины остаточной деформации при растяжении принято остаточное удлинение 0,2 %. Эта величина называется условным пределом текучести:

где Pq 2 — нагрузка при условном пределе текучести.

При увеличении напряжений сверх предела текучести при растяжении в результате сильной деформации происходит упрочнение металла (изменение его структуры и свойств) и сопротивление деформации увеличивается, поэтому за участком текучести, т. е. за точкой 3, наблюдается подъем кривой растяжения (участок упрочнения). До точки 4 удлинение образца происходит равномерно. Наибольшее значение нагрузки, предшествовавшее разрушению образца, обозначим Р_макс. Точка 4 характеризует максимальное условное напряжение, возникающее в процессе испытания, называемое временным сопротивлением.

Временное сопротивление а_в — условное напряжение, определяемое по отношению действующей силы к исходной площади поперечного сечения образца и отвечающее наибольшей нагрузке ^макс’ предшествовавшей разрушению образца:

В момент, соответствующий нагрузке Р_макс, появляется заметное местное сужение образца (шейка). Если до этого момента образец имел цилиндрическую форму, то теперь растяжение образца сосредоточивается в области шейки.

Участку 4—5 соответствует быстрое уменьшение сечения шейки, вследствие чего растягивающая сила уменьшается, хотя напряжение растет (площадь сечения в шейке ^_вр Fq).

При дальнейшей деформации шейка сужается и образец разрывается по наименьшему сечению F_K, где напряжения в действительности достигают наибольшей величины. Таким образом, нарастание пластической деформации при растяжении происходит поэтапно: равномерная пластическая деформация до точки 4 и местная пластическая деформация от точки 4 до точки 5 — момента разрушения.

Моменту разрыва соответствует точка 5, усилие разрыва обозначим Р_к. Отношение разрывающего усилия к действительной площади сечения в месте разрыва называется истинным сопротивлением разрыву:

У пластичных металлов P/Fq, где / и Fq — первоначальные длина и площадь сечения образца. Диаграмма в координатах «напряжения — деформации» на участке 4—5 является условной, как было указано выше. При напряжении, соответ-

Рис. 2.4. Диаграмма истинных напряжений ствующем временному сопротивлению (точка 4), образуется шейка и площадь сечения резко уменьшается, поэтому истинное напряжение увеличивается и истинная диаграмма 4—5′ расположена выше условной диаграммы 4—5.

Следует отметить, что временное сопротивление не совпадает с сопротивлением разрыву и оказывается меньше последнего. Истинное сопротивление разрыву получается делением наибольшей нагрузки Р_пч (точка 4′) на истинную уменьшенную площадь сечения F_Bp в момент начала появления шейки.

Таким образом, истинные напряжения с увеличением деформации непрерывно растут до момента разрушения образца.

Показателем пластической деформации является его абсолютное остаточное удлинение А/_0Ст.п П Р И разрыве (отрезок ОЛ[ на рис. 2.3), так как упругая деформация (отрезок A^₂) исчезает после разрыва:

где / — начальная длина образца, /_к — конечная длина образца (рис. 2.5).

Общее удлинение образца при растяжении слагается из равномерного и сосредоточенного удлинения (за счет образования шейки). Так как размеры испытуемых образцов могут быть различными, то характеристикой пластичности образца служит не его абсолютное, а относительное остаточное удлинение при разрыве 6 — отношение приращения расчетной длины образца после разрыва к первоначальной расчетной длине / в процентах:

Чем больше 5, тем пластичнее металл.

Рис. 2.5. Образцы до растяжения (а) и после растяжения (б)

Другой характеристикой пластичности металла является относительное сужение сечения ц/ после разрыва (в процентах) — отношение разности начальной площади и минимальной площади поперечного сечения образца разрыва к начальной площади поперечного сечения образца.

Если Fq — начальная площадь образца, F_K — минимальная площадь сечения в месте образования шейки (в месте разрыва), то относительное сужение (в процентах)

При оценке свойств образцов пластических материалов большое значение имеет их сопротивление пластической деформации. Оно показывает, какое напряжение можно допустить, не вызывая (или вызывая допускаемую величину) пластической деформации, т. е. изменения металла под действием внешних сил.

Свойства, характеризующие сопротивление пластической деформации, можно разделить на две группы: сопротивление металла малым пластическим деформациям и сопротивление металла значительным пластическим деформациям.

Величиной, характеризующей сопротивление малым пластическим деформациям, является предел упругости. Свойства сопротивления металла значительным пластическим деформациям проявляются при напряжениях выше условного предела текучести. Для пластических металлов временное сопротивление определяет сопротивление их значительным пластическим деформациям. Временное сопротивление является основной характеристикой хрупких материалов, разрушающихся при малых пластических деформациях.

В табл. 2.1 приведены механические характеристики некоторых материалов.

Диаграмма растяжения стали марки Ст3

Рассмотрим характерные участки и точки диаграммы растяжения малоуглеродистой стали, а также соответствующие им стадии деформирования образца (рис. 2.2).

От начала нагружения до определенного значения растягивающей силы имеет место прямая пропорциональная зависимость между силой и удлинением образца. Эта зависимость выражается на диаграмме прямой ОА. На этой стадии растяжения справедлив закон Гука. Обозначим силу, при которой закон пропорциональности прекращает свое действие, через Р_пц. Этому значению силы на диаграмме соответствует точка А. Напряжение, вызванное силой Р_пц, называется пределом пропорциональности и вычисляется по формуле: s_пц = Р_пц/F.

Пределом пропорциональностиs_пц называется напряжение, после которого нарушается закон Гука. Для Ст3 s_пц » 200 МПа.

Деформация называется упругой, если она полностью исчезает после разгрузки. Постепенно повышая нагрузку, будем проводить полную разгрузку образца. Пока сила Р не достигнет определенной величины, вызванные ею деформации будут исчезать при разгрузке. Процесс разгружения при этом изобразится той же линией, что и нагружение. Обозначим через Р_у наибольшее значение силы, при котором образец еще не дает при разгрузке остаточной деформации. Этому значению на диаграмме соответствует точка В, а упругой стадии растяжения образца — участок ОВ.

Наибольшее напряжение, до которого остаточная деформация образца не обнаруживается при разгрузке, называется пределом упругости s_у = Р_у /F. Обычно за предел упругости принимают напряжение, при котором остаточная деформация достигает 0,001¸0,005 %. При этом предел упругости обозначается через s_0,001 или s_0,005. Для Ст3 s_у » 210 МПа.

Далее кривая плавно поднимается до точки C, где наблюдается переход к горизонтальному участку CD, называемому площадкой текучести. На этой стадии удлинение образца растет при постоянном значении растягивающей силы, обозначаемой Р_т. Такой процесс деформации называется текучестью материала.

Пределом текучестиназывается наименьшее напряжение, при котором деформация образца происходит при постоянном растягивающем усилии, s_т = Р_т /F. Для Ст3 s_т = 240 МПа.

После стадии текучести материал вновь приобретает способность увеличивать сопротивление дальнейшей деформации. Этому процессу соответствует восходящий участок DE диаграммы, называемый участком упрочнения. Точка E соответствует наибольшему усилию Р_max, которое может воспринять образец.

Напряжение, соответствующее максимальной силе Р_max, называется временным сопротивлением или пределом прочности s_в = Р_max /F. Для Ст3 s_В » 400 МПа.

После достижения усилия Р_max деформация происходит на небольшой длине образца. Это ведет к образованию местного сужения в виде шейки и к падению силы Р, не смотря на то, что напряжение в сечении шейки непрерывно растет.

Обозначив через Р_к величину растягивающей силы в момент разрыва, получим:

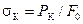. (2.1)

Если в процессе растяжения дойти до некоторой точки М, напряжение для которой выше предела упругости, а затем начать разгрузку, то линия разгрузки будет выражаться прямой MN, параллельной начальному участку диаграммы OB. При полном снятии нагрузки в образце сохраняется остаточная деформация Dl_ост. Полная деформация испытываемого образца состоит из двух частей:

,

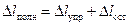где Dl_упр — упругая деформация, исчезающая после снятия нагрузки; Dl_ост — остаточная деформация.

После испытания образца определяют относительное остаточное удлинение при разрыве:

,

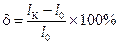и относительное остаточное сужение в шейке:

,

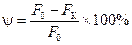где l_К и F_К — длина образца и площадь поперечного сечения в шейке после разрыва. Величины d и y являются характеристиками пластичности материала. Для Ст3 d = 21¸27 %; y = 60¸70 %.

Разделив нагрузку P на начальную площадь поперечного сечения F, а абсолютное удлинение Dl на расчетную длину образца l, получим так называемую диаграмму напряжений в координатах s-e (рис. 2.3), вид которой совпадает с диаграммой растяжения. Из диаграммы видно, что:

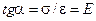, (Закон Гука)

где Е — модуль продольной упругости (модуль упругости первого рода, модуль Юнга).

Если в ходе испытания измерять поперечную деформацию e¢ и следить за изменением отношения e¢/e, то можно обнаружить, что в зоне малых упругих деформаций это отношение останется практически постоянным. Величину 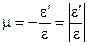называют коэффициентом поперечной деформации или коэффициентом Пуассона. Величины Е и m характеризуют упругие свойства материалов, поэтому их называют упругими постоянными. Для Ст3 Е = 2×10 5 МПа; m = 0,3.

Нисходящий участок ЕК диаграммы напряжений носит условный характер, поскольку площадь поперечного сечения образца непрерывно уменьшается после образования шейки. Деля величину силы на действительную площадь поперечного сечения образца F_i, можно построить истинную диаграмму напряжений. Истинное сопротивление в момент разрыва определяется .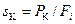

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Диаграммы упруго-пластического деформирования конструкционных материалов

Основным опытом для определения механических характеристик конструкционных материалов является опыт на растяжение призматического образца центрально приложенной силой, направленной по продольной оси; при этом в средней части образца реализуется однородное напряженное состояние.

Форма, размеры образца и методика проведения испытаний определяются соответствующими стандартами, например, ГОСТ 34643—81, ГОСТ 1497-73. По результатам испытаний строится зависимость σ=f (ε) между напряжениями σ=F/A и деформациями ε=Δl/l , которая называется диаграммой деформирования.

Опыты на растяжение образцов выявляют некоторые общие свойства конструкционных материалов—свойства упругости и пластичности. Рассмотрим типичные кривые деформирования при растяжении образцов из материала сталь 30 и сталь 40Х.

Характерные диаграммы растяжения

Если напряжения не превышают предела пропорциональности (первая точка на диаграмме), и зависимость между напряжениями и деформациями линейна, то она описывается законом Гука σ=εЕ , где Е — модуль продольной упругости материала. Размерность модуля упругости — Н/м 2 (Паскаль). Значение модуля упругости Е на кривой деформирования численно равно тангенсу угла наклона линейного участка: Е = tgβ. Таким образом, величину Е можно рассматривать как характеристику упругого сопротивления или как характеристику интенсивности — нарастания напряжения с увеличением деформации.

Физический смысл коэффициента Е определяется как напряжение, необходимое для увеличения длины образца в два раза. Такое толкование довольно искусственно, поскольку величина упругого удлинения у большинства твердых тел редко достигает даже 1%.

Напряжения, являющиеся верхней границей проявления чисто упругих деформаций, соответствуют точке 2 диаграммы и называются пределом упругости σ_упр .

Точка 3 диаграммы характерна тем, что при достижении напряжениями величины σ = σ_т ( σ_т — предел текучести), дальнейшее удлинение образца (для малоуглеродистых сталей) происходит практически без увеличения нагрузки. Это явление носит название текучести, а участок диаграммы, расположенный непосредственно правее точки 3, называется площадкой текучести. При этом полированная поверхность образца мутнеет, докрывается ортогональной сеткой линий (линии Чернова—Людерса), расположенных под углом 45 o к продольной оси образца—по направлению плоскостей действия максимальных касательных напряжений.

У многих конструкционных материалов площадка текучести не выражена столь явно, как у малоуглеродистых сталей. Для таких материалов вводится понятие условного предела текучести σ_s; это напряжение, которому соответствует остаточная (пластическая) деформация, равная s %. Обычно принимается s = 0,2%. Поэтому условный предел текучести часто обозначается как σ_0,2.

После площадки текучести для дальнейшего увеличения деформации необходимо увеличение растягивающей силы. Материал снова проявляет способность сопротивляться деформации; участок за площадкой текучести (до точки 4) называется участком упрочнения. Точка 4 соответствует максимальной нагрузке, выдерживаемой образцом. Соответствующее напряжение называется временным сопротивлением σ_в (или пределом прочности σ_пч ).

Дальнейшая деформация образца происходит без увеличения или даже с уменьшением нагрузки вплоть до разрушения (точка 5). Точке 4 на диаграмме соответствует начало локального уменьшения размеров поперечного сечения образца, где, в основном, сосредоточивается вся последующая пластическая деформация.

Диаграмма, приведенная на рисунке выше, является диаграммой условных напряжений, условность состоит в том, что все силы относились к первоначальной площади поперечного сечения образца; в действительности же при растяжении площадь поперечного сечения образца уменьшается. Если учитывать текущее значение площади поперечного сечения при определении напряжений, то получим диаграмму истинных напряжений.

Диаграмма истинных напряжений

Если в некоторый момент нагружения (точка А на рисунке «Характерные диаграммы растяжения») прекратить нагружение и снять нагрузку, то разгрузка образца пойдет по линии АВ, параллельной линейному участку диаграммы 0—1. При этом полная деформация в точке А равна:

ε =ε (е) + ε (р)

где ε (е) = σ/Е — упругая деформация, ε (р) — пластическая (остаточная деформация). Уравнение это справедливо для любой точки диаграммы.

Эффект Баушингера. После того как материал испытал воздействие осевого усилия одного знака (например, растяжение) в области пластических деформаций (σ>σ_т), сопротивляемость этого материала пластической деформации при действии сил другого знака (сжатие) понижается. Это явление носит название эффекта Баушингера.

При растяжении образца происходит не только увеличение его длины, но и уменьшение размеров поперечного сечения, т. е. в упругой области деформация в поперечном направлении ε’ = -με, где ε— деформация в продольном направлении, μ— коэффициент Пуассона. Для изотропных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 .

Характеристиками пластичности материала являются относительное удлинение δ и относительное сужение ψ при разрыве:

,где l, А — длина рабочей части образца и площадь поперечного сечения до деформации; l_к — длина рабочей части образца после разрыва; А_К — конечная площадь поперечного сечения в шейке образца после разрыва.

По величине относительного удлинения δ при разрыве проводится разделение состояния материалов на пластичное и хрупкое. Материалы, имеющие к моменту разрушения достаточно большие значения δ>10%, относят к пластическим материалам; к хрупким относят материалы с относительным удлинением δ 2 или см 2 ].

Работа деформации W при разрушении образца может быть определена по диаграмме растяжения σ=f (ε). Так, если первоначальная длина образца l, то работа деформации, совершаемая силой F на перемещении и:

где u_к — перемещение в момент, предшествующий разрушению. Тогда по зависимости σ= F/A=f (ε) и ε=u/l, находим

где W₁— площадь диаграммы деформирования (работа деформации на единицу объема материала).

Для сталей ударная вязкость 50—100 Н·м/см 2 . Материалы с ударной вязкостью менее 30 Н· м/см 2 относят к числу хрупких.

Некоторые пластичные материалы в районе площадки текучести обнаруживают особенность (например, титан), называемую «зубом текучести»; для таких материалов вводится понятие верхнего и нижнего предела текучести.

Экспериментальное изучение свойств материалов при сжатии проводится на коротких образцах с тем, чтобы исключить возможность искривления образца. Для пластичных материалов характер диаграммы σ=f (ε при сжатии примерно до возникновения текучести такой же, как и при растяжении. В процессе деформации сжатия образец укорачивается; при этом размеры поперечного сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так как образец сплющивается.

Хрупкие материалы проявляют значительно лучшую способность сопротивляться деформациям сжатия, чем деформациям растяжения; для них разрушающее напряжение при сжатии превышает предел прочности при растяжении в несколько раз. Разрушение хрупких материалов при сжатии происходит за счет образования трещин.

Диаграмма растяжения различных материалов

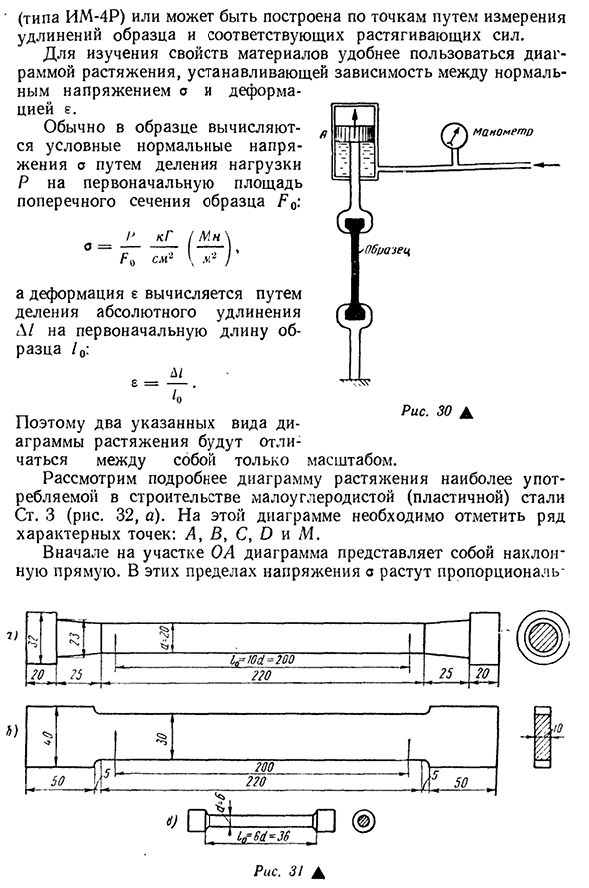
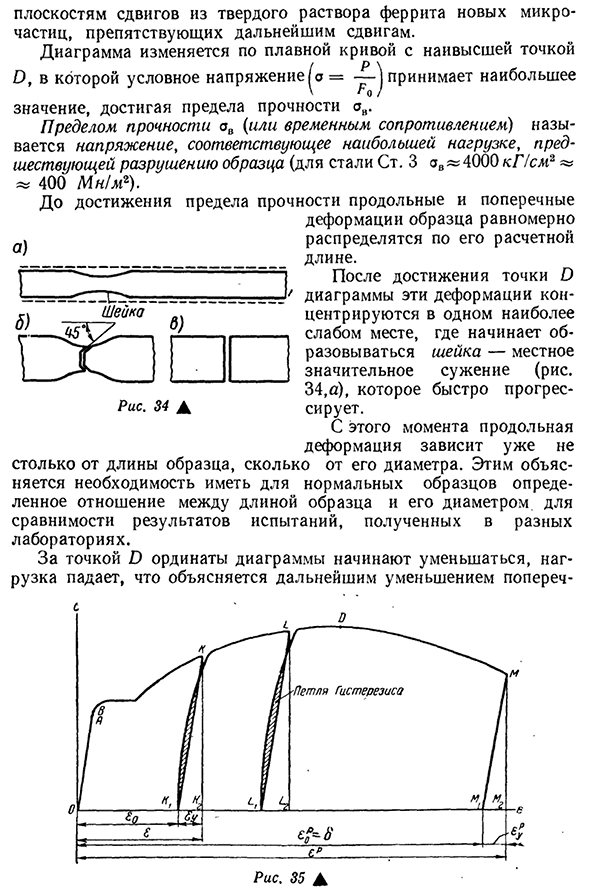
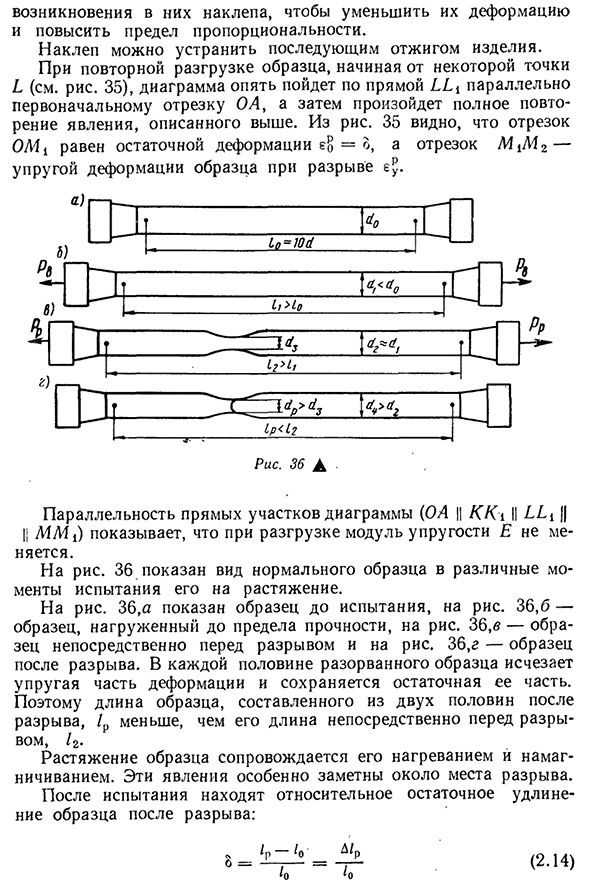
Диаграмма растяжения

• Растянуть диаграмму Для детального изучения «поведения» различных материалов под нагрузкой лабораторные испытания образцов, изготовленных из этих материалов, проводятся на специальных испытательных машинах. Эти испытания проводятся для определения числовых характеристик, для оценки прочности и пластичности материала. Такую характеристику обычно называют механической. Тестовая машина оснащена устройством, которое

показывает величину нагрузки, передаваемой образцу. Удлинение образца устанавливается специальным измерительным прибором. Есть машина, которая автоматически строит удлинение образца в зависимости от нагрузки. Среди таких машин есть, например, машина IM-4R, выпускаемая на нашем заводе. Общий вид этой машины показан на рисунке. 29.

В испытательной машине предел прочности образца создается механическим или гидравлическим Людмила Фирмаль

устройством. Это 31-й 29А Для риса. На рисунке 30 показана принципиальная схема машины с гидравлической системой. Масло впрыскивается в цилиндр А, который поднимает поршень и растягивает образец. Значение растягивающего усилия можно определить по давлению, измеренному манометром. Для сравнения результатов испытаний, проведенных в разных лабораториях, были определены тип и размер выборки. Для риса. 31, a и b представляют

круглые (нормальные) и плоские образцы, используемые в Советском Союзе при испытаниях на растяжение металла. Расчетная длина нормального образца равна расстоянию между рисками, приложенными к цилиндрической части / 0 = 10d == 200 мм. * В некоторых случаях используются так называемые небольшие образцы (рис. 31, Б), которые были испытаны на небольшой машине типа IM-4P. Испытание материала на растяжение особенно важно, и

• свойства материала и его свойства наиболее полно раскрыты. График зависимости между растягивающей силой P и удлинением образца A / называется растягивающей диаграммой. Телескопические чертежи автоматически отрисовываются самописцем история * Если по какой-либо причине невозможно сделать обычный образец, используйте образец диаметром 15 или 10 мм с таким же соотношением длины к диаметру. 32 (тип IM-4P) может быть построен в точке или путем измерения образца и соответствующего удлинения при растяжении. Для изучения свойств материала удобнее использовать диаграмму растяжения, которая устанавливает связь между нормальным

напряжением o и деформацией E. Как правило, для образца условное нормальное напряжение o рассчитывается путем деления нагрузки P на начальную площадь поперечного сечения образца f o. : Деформация e рассчитывается путем деления абсолютного удлинения L / на исходную длину образца / 0: тонна — Два упомянутых типа напряженности связаны только по масштабу. Рис 30л Поэтому низкоуглеродистая (пластиковая) сталь ст.3 (рис. 32, а). На этом рисунке нам нужно обратить внимание на некоторые характерные точки A, B, C, D и M. В начале графика ОА фигура представляет собой диагональную прямую линию. В этих пределах напряжение

растет пропорционально Рис 31а 2 Порядок № 1037 пропорционален деформации e, т. Е. Наблюдается крючковый метод, который Людмила Фирмаль

соответствует пределам пропорциональности APC. Пропорциональный предел APC — это максимальное напряжение, при котором действует закон Крюка (Сталь St.3APC «» 2100 кг! SMG®210M «LI2). Касательная к горизонтальной оси угла наклона прямой части ОА равна модулю упругости: В нарушение точки А, кривой диаграммы и закона Хука выше деформация начинает расти быстрее, чем возрастает напряжение. Вы можете отметить точку B, которая очень близка к точке A на графике кривой на рисунке и соответствует пределу упругости AUP. Предел упругости AUP — это максимальное напряжение, которое материал может выдержать без каких-либо признаков остаточной деформации во время разгрузки *. Поскольку точка B близка к точке A, ее часто считают совпадением. Если вы проведете вертикальную линию через точку B, с левой стороны этой

линии на диаграмме будет зона упругой деформации, а справа — зона упругой пластической деформации (упругая деформация и пластическая деформация). Начиная с некоторой точки C, есть горизонтальный (или почти горизонтальный) участок, соответствующий диаграмме история * По ГОСТ условным пределом для упругости st05 является напряжение, при котором остаточная деформация достигает 0,05%. Если в технических условиях имеются специальные указания, то остаточное удлинение считается меньшим. 34 от предела текучести. В этой области деформация увеличивается без увеличения нагрузки, и материал, кажется, течет. Предел текучести