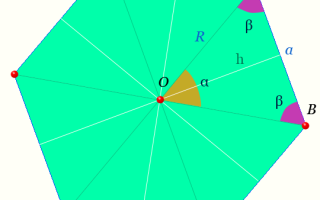
Какой угол в правильном шестиугольнике?

Правильный шестиугольник и его свойства: читаем по порядку

Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.

Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA, OB — радиусы правильного шестиугольника.

Свойства

Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности (), поскольку .
Все углы равны 120°.
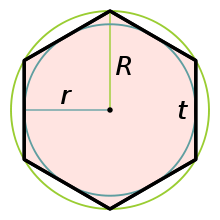
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:

Шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра 1 можно покрыть правильным шестиугольником со стороной (лемма Пала).

Свойства правильного шестиугольника

все внутренние углы равны между собой
каждый внутренний угол правильного шестиугольника равен 120 градусам
все стороны равны между собой
сторона правильного шестиугольника равна радиусу описанной окружности
большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
меньшая диагональ правильного шестиугольника в ( sqrt <3>)раз больше его стороны.
vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
правильный шестиугольник заполняет плоскость без пробелов и наложений
диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ):

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)

Радиус вписанной окружности правильного шестиугольника равен апофеме:

(r = m = alargefrac<><2>normalsize)

Радиус описанной окружности равен стороне правильного шестиугольника:

Периметр правильного шестиугольника

Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны

(S = pr = largefrac<<3sqrt 3 >><2>normalsize),
где (p) − полупериметр шестиугольника.

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности

Построение

Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.

Интересные факты

Как известно, пчелы строят соты правильной шестиугольной формы. Дело в том, что шестиугольник – самая оптимальная геометрическая форма для максимально полезного использования единицы площади. Шестиугольник близок к кругу – идеальной естественной фигуре, – но у него есть преимущество: вплотную примыкая друг к другу, шестиугольники позволяют использовать всю полезную площадь сот, максимально заполняя ее медом. Совсем не так было бы, если бы ячейки имели круглую форму – между ними неизбежно оставалось бы много пространства, которое невозможно использовать.
Панцирь черепахи состоит из шестиугольников. Благодаря ячейкам такой формы он проще всего наращивается. Черепахи растут, и их панцирь должен увеличиваться вместе с ними, причем равномерно по всей площади. Поэтому черепаший панцирь формируется из отдельных пластинок, плотно пригнанных друг к другу, как дощечки паркета, но сохраняющих способность прирастать по краям. Если бы пластинки могли равномерно расти во все стороны, они имели бы форму кругов. Однако круги не могут плотно прилегать друг к другу, между ними неизбежно будут оставаться просветы.
Некоторые сложные молекулы углерода (напр., графит) имеют гексагональную кристаллическую решётку.
Гигантский гексагон — атмосферное явление на Сатурне.
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Гексаграмма — шестиконечная звезда, образованная двумя равносторонними треугольниками. Является, в частности, символом иудаизма.
Контур Франции напоминает правильный шестиугольник, поэтому он является символом страны.

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

Правильный шестиугольник в природе, технике и культуре

Слева направо:
Пчелиные соты;
Графен — одна из аллотропных модификаций углерода;
Гигантский гексагон.

Шестиугольник, виды, свойства и формулы

Шестиугольник, виды, свойства и формулы.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник

Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Правильный шестиугольник (понятие и определение):

Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник

Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.

Углы правильного шестиугольника образуют шесть равносторонних треугольников .

Правильный шестиугольник можно построить с помощью циркуля и линейки.

Свойства правильного шестиугольника:

1. Все стороны правильного шестиугольника равны между собой.

2. Все углы равны между собой и составляют 120°.

Рис. 4. Правильный шестиугольник

3. Сумма внутренних углов любого правильного шестиугольника равна 720°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник

5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

Рис. 7. Правильный шестиугольник

7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).

8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Правильный шестиугольник

Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.

Содержание

Свойства

Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности (), поскольку .
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:

Шестиугольники замещают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра 1 можно покрыть правильным шестиугольником со стороной (лемма Пала) [1] .

Построение

Правильный шестиугольник в природе, технике и культуре

Примечания

↑А. М. РайгородскийПроблема Борсука. — М .: Издательство МЦНМО, 2006. — С. 9. — 56 с. — (Библиотека „Математическое просвещение“). — ISBN ISBN 5-94057-249-9

Смотрите также

Шестиугольник
Упаковка кругов на плоскости

Ссылки

Правильные многоугольники
Основные	Треугольник • Квадрат • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Семнадцатиугольник • 257-угольник • 65537-угольник
См. также	Многоугольник • Теорема Гаусса — Ванцеля

Wikimedia Foundation . 2010 .

Яхдун-Лим
Блатт, Дэвид

Смотреть что такое «Правильный шестиугольник» в других словарях:

Шестиугольник — Правильный шестиугольник Шестиугольник многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Сумма внутренних углов выпуклого шестиугольника р … Википедия

Шестиугольник Сатурна — Гексагональное устойчивое атмосферное образование на северном полюсе Сатурна, открытое аппаратом Вояджер 1 и наблюдаемое снова в 2006 году а … Википедия

Правильный многоугольник — Правильный семиугольник Правильный многоугольник это выпуклый многоугольник, у которого все стороны и углы равны . Определение правильного многоугольника может зависеть от определения … Википедия

Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия

Правильный треугольник — Правильный треугольник. Правильный (или равносторонний) треугольник это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны … Википедия

Правильный девятиугольник — это правильный многоугольник с девятью сторонами. Свойства Правиль … Википедия

Правильный 17-угольник — Правильный семнадцатиугольник геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание 1… … Википедия

Правильный семнадцатиугольник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание … Википедия

Правильный восьмиугольник — (октагон) геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой … Википедия

Правильный 65537-угольник — 65537 угольник или окружность? Правильный 65537 угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиугольник) геометрическая фигура из группы правильных многоугольников, состоящая из 65537 … Википедия

Шестиугольник, виды, свойства и формулы

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым и невыпуклым.

Рис. 1. Выпуклый шестиугольник

Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Чем он отличается от неправильного?

Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.

В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.

В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.

Правильный шестиугольник (понятие и определение):

Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Рис. 3. Правильный шестиугольник

Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.

Углы правильного шестиугольника образуют шесть равносторонних треугольников.

Правильный шестиугольник можно построить с помощью циркуля и линейки.

Свойства правильного шестиугольника:

1. Все стороны правильного шестиугольника равны между собой.

a1 = a2 = a3 = a4= a5= a6.

2. Все углы равны между собой и составляют 120°.

α1 = α2 = α3 = α4 = α5 = α6 = 120°.

Рис. 4. Правильный шестиугольник

3. Сумма внутренних углов любого правильного шестиугольника равна 720°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник

5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник

6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.

Рис. 7. Правильный шестиугольник

8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Рис. 8. Правильный шестиугольник

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

диаметр описанной окружности;
диаметр вписанной окружности;
площадь;
периметр.

Описанная окружность и возможность построения

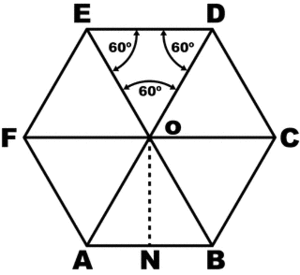
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

R=а.

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

S=πR²

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

Правильный шестиугольник в природе, технике и культуре:

Пчелиные соты имеют форму правильного шестиугольника.

Графит, графен имеют гексагональную кристаллическую решетку.

Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне

Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.

Панцирь черепахи состоит из шестиугольников.

Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции

Формулы правильного шестиугольника:

Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.

Формулы периметра правильного шестиугольника:

Формулы площади правильного шестиугольника:

Формула радиуса окружности, вписанной в правильный шестиугольник:

Формула радиуса окружности, описанной вокруг правильного шестиугольника:

Правильный шестиугольник

Знаете ли вы, как выглядит правильный шестиугольник? Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.

Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.

Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.

Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?

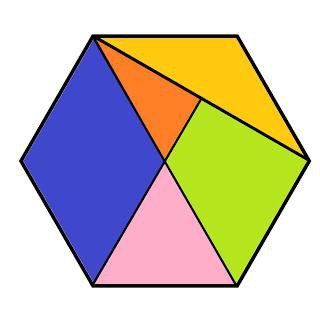
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.

Мы знаем, что площадь правильного треугольника: .

Тогда площадь правильного шестиугольника — в шесть раз больше.

, где — сторона правильного шестиугольника.

Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.

Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне. Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти. Он равен . Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.

Ты нашел то, что искал? Поделись с друзьями!

. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Радиус такой окружности равен .

. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

Звоните нам: 8

(бесплатный звонок по России)
+7
(бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

Обучающее видео БЕСПЛАТНО

Техническая поддержка: [email protected] (круглосуточно)

Закажите звонок и получите скидку -50% на первый месяц занятий!

Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная практика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.

Что такое правильный шестиугольник и какие задачи с ним могут быть связаны

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

чертится прямая линия и на ней ставится точка;
из этой точки строится окружность (она является ее центром);
из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
после этого отрезками последовательно соединяются все точки на первой окружности.

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Особенности инструмента с плоским наконечником

Прямошлицевая или, по-другому, плоская отвертка обычно маркируется несколькими латинскими символами SL. Основное предназначение – это ввинчивать либо выкручивать винты, имеющие на головки одну прямую прорезь. Стоит отметить, что такие метизы не способны выдерживать большие нагрузки. Чаще всего применяют его для мелкого бытового ремонта.

Плоская отвертка не позволяет плотно ввинтить винт, так как своеобразная головка не дает возможности туго затянуть крепление. При сильном нажатии на метиз нередко срезается шлиц инструмента. Приржавевший же винт открутить плоской отверткой не всегда удается.

Свойства правильного шестиугольника

(по порядку следования формул)

Радиус описанной окружности (R) правильного шестиугольника равен его стороне (t)
Все внутренние углы равны 120 градусам
Радиус вписанной окружности (r) равен корню из трех, деленному на два и умноженному на длину стороны t (радиус описанной окружности R)
Периметр правильного шестиугольника (P) равен шести радиусам описанной окружности (R) или четыре корня из трех, умноженным на радиус вписанной окружности (r)
Площадь правильного шестиугольника равна трем корням из трех пополам, умноженным на квадрат радиуса описанной окружности (R) или квадрат стороны (t); либо площадь правильного шестиугольника равна двум корням из трех, умноженным на квадрат радиуса вписанной окружности (t)

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.

Правильный шестиугольник в природе, технике и культуре:

Пчелиные соты имеют форму правильного шестиугольника.

Графит, графен имеют гексагональную кристаллическую решетку.

Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне

Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Панцирь черепахи состоит из шестиугольников.

Рис. 10. Материковая часть Франции

Правильный шестиугольник

В случае, если шестиугольник имеет правильную форму, то расчет нужного параметра становится гораздо проще.

Умножьте длину его стороны на 6 и вы получите нужное значение по формуле P=a*6, где a — сторона правильного шестиугольника.
Например, у нас имеется фигура со стороной длиной 10 сантиметров, умножаем 10 на 6 и получаем в итоге 60 сантиметров в периметре.
Также правильная фигура имеет уникальное свойство: радиус окружности, который описан вокруг такого шестиугольника, равен длине его стороны. Если вам известен радиус описанной окружности, то достаточно воспользоваться формулой в виде P=R*6, где R — радиус описанной окружности.

Например, известен прямоугольник, вписанный в окружность, имеющую диаметр 20 сантиметров. Тогда радиус будет в два раза меньше и составит 10 сантиметров. Полученную величину умножаем на 6 сторон и получаем периметр.

Какие свойства требуется знать при решении задач?

К тому, что указано выше, следует добавить:

диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.

Объем призмы

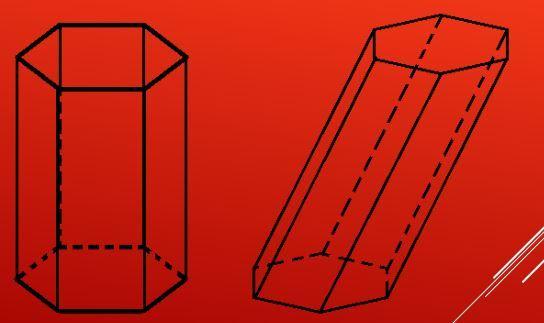
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:

Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.

голоса

Рейтинг статьи

Читать еще: Цинкование с паяльной кислотой в домашних условиях